Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
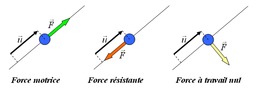
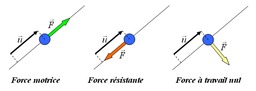
Cas particuliers du travail d'une force
Trois cas particuliers du travail d'une force : force motrice, force résistante, force à travail nul. Considérons une force vec{F} constante s'appliquant sur un objet se déplaçant sur une trajectoire rectiligne (Il n'y a pas d'autres forces s'exerçant sur l'objet). Un certain nombre de cas particuliers permettent d'illustrer la notion de travail d'une force : Si la force vec{F} est parallèle au déplacement vec{u} et orientée dans le même sens, le travail W = vec{F}cdotvec{u} fourni par la force est positif : d'après le théorème de l’énergie cinétique, la force a augmenté l'énergie cinétique du système, celui-ci se déplace donc plus rapidement. Une telle force est parfois dénommée force motrice. Si la force vec{F} est parallèle au déplacement vec{u} mais orientée dans le sens opposé, le travail W = vec{F}cdotvec{u}, fourni par la force est négatif : d'après le théorème de l’énergie cinétique, la force a diminué l'énergie cinétique du système, celui-ci se déplace donc plus lentement. On appelle parfois une telle force, une force résistante. Si la force vec{F} est perpendiculaire au déplacement vec{u}, le travail de la force est nul W = 0 : la force n'a pas modifié l'énergie cinétique du système. On peut dire plus simplement que si la force vec{F} est perpendiculaire au déplacement, elle ne modifie pas le déplacement. Ce dernier cas ne doit pas laisser penser qu'une force dont le travail est nul n'a aucun effet sur un système. Les forces dont le travail est nul ne modifient pas l'énergie cinétique du solide. En particulier, elles ne modifient pas la norme de la vitesse ; elles peuvent cependant en modifier la direction.
Contes, Textes, Force motrice, Boeufs, Pari, Djataka, Bouviers, Concours et compétitions, Maltraitance des animaux
L'histoire du boeuf qui gagna le prix
Conte de Djataka, "L'histoire du boeuf qui gagna le prix", traduction Annie Lesca. 518 mots. Narration et dialogues.
Travail d'une force
Le travail d'une force est l'énergie fournie par cette force lorsque son point d'application se déplace (l'objet subissant la force se déplace ou se déforme). Il est responsable de la variation de l'énergie cinétique du système qui subit cette force. Si par exemple on pousse une voiture, le travail de la poussée est l'énergie produite par cette poussée. Considérons une force vec{F} constante s'appliquant sur un objet se déplaçant sur une trajectoire rectiligne (Il n'y a pas d'autres forces s'exerçant sur l'objet). Un certain nombre de cas particuliers permettent d'illustrer la notion de travail d'une force : 1) Si la force vec{F} est parallèle au déplacement vec{u} et orientée dans le même sens, le travail W = vec{F}cdotvec{u} fourni par la force est positif : d'après le théorème de l’énergie cinétique, la force a augmenté l'énergie cinétique du système, celui-ci se déplace donc plus rapidement. Une telle force est parfois dénommée force motrice. 2) Si la force vec{F} est parallèle au déplacement vec{u} mais orientée dans le sens opposé, le travail W = vec{F}cdotvec{u}, fourni par la force est négatif : d'après le théorème de l’énergie cinétique, la force a diminué l'énergie cinétique du système, celui-ci se déplace donc plus lentement. On appelle parfois une telle force, une force résistante. 3)Si la force vec{F} est perpendiculaire au déplacement vec{u}, le travail de la force est nul W = 0 : la force n'a pas modifié l'énergie cinétique du système. On peut dire plus simplement que si la force vec{F} est perpendiculaire au déplacement, elle ne modifie pas le déplacement.