Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.

Votre recherche ...

Nuage de mots clés

Bouteilles | Mathématiciens | Ferdinand Möbius (1790-1868) | Felix Klein (1849-1925) | Dessins et plans | Géométrie | Rubans | Photographie | Noeuds et épissures | Travail du verre | Mathématiques récréatives |
Bouteille de Klein. Source : http://data.abuledu.org/URI/52f2bcd5-bouteille-de-klein

Dessins et plans, Géométrie, Rubans, Bouteilles, Mathématiciens, Ferdinand Möbius (1790-1868), Felix Klein (1849-1925)

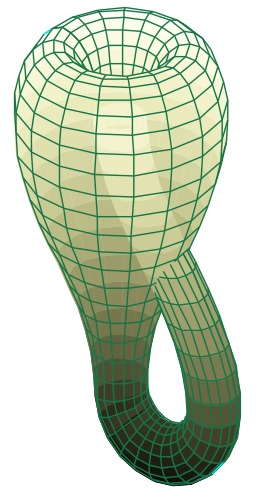
Bouteille de Klein

Vue de la bouteille de Klein dans un espace à trois dimensions. En mathématiques, la bouteille de Klein (prononcé kla.in) est une surface fermée, sans bord et non orientable, c'est-à-dire une surface pour laquelle il n'est pas possible de définir un « intérieur » et un « extérieur ». La bouteille de Klein a été décrite pour la première fois en 1882 par le mathématicien allemand Felix Klein (1849-1925). Elle est étroitement liée au ruban de Möbius.

→

Bouteille de Klein en verre. Source : http://data.abuledu.org/URI/52f2be44-bouteille-de-klein-en-verre

Photographie, Bouteilles, Mathématiciens, Noeuds et épissures, Travail du verre, Mathématiques récréatives, Ferdinand Möbius (1790-1868), Felix Klein (1849-1925)

Bouteille de Klein en verre

Réalisation de l'immersion de la bouteille de Klein, en verre. On peut en quelque sorte considérer que la bouteille de Klein est une surface qui fait un « nœud ». En tant que surface (objet à 2 dimensions), il lui faut 4 dimensions pour faire un nœud, de même que pour une courbe (objet à une dimension) il faut 3 dimensions pour faire un nœud.

→