Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géographie antique -- Cartes, Claude Ptolémée (0100?-0170?), Géographie antique, Proche-Orient (Jusqu'à 622), Villes disparues, en ruine, etc. -- Proche-Orient
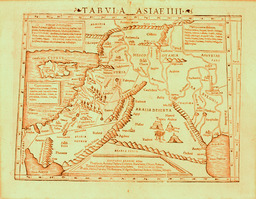
Carte de l'Asie de Ptolémée
Quatrième planche de l'Asie, de Ptolémée (TABULA ASIAE IIII), de l'île de Chypre à gauche, jusqu'à l'Assyrie à droite. Légende en latin.
Dessins et plans, Cartes du monde, Géographie antique -- Cartes, Claude Ptolémée (0100?-0170?), Géographie antique, Géographie historique
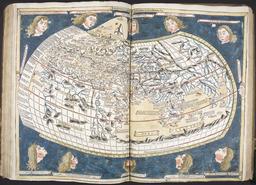
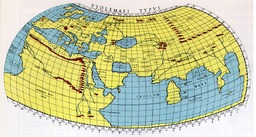
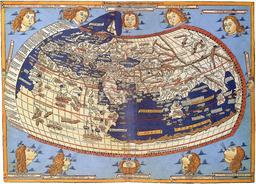
Carte du monde de Ptolémée
Carte du monde d'après Claude Ptolémée, "Cosmographia", publiée en 1482.
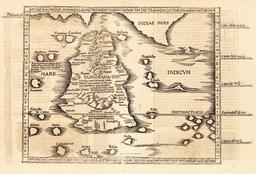
L'île de Ceylan
Ptolémée dénombre 1378 îles qui entourent Trapobena (mot sanskrit "tamraparni" qui désignait une "feuille de cuivre"). À son époque les habitants sont les Salai et l'île s'appelle Salika, alors qu'avant ils appelaient l'île Symondi ou encore Palaisimoundou.
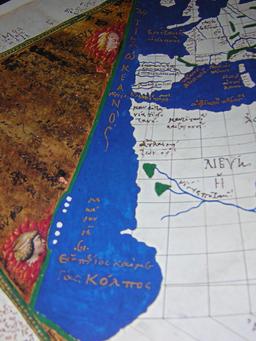
L'océan atlantique de Ptolémée
Détail de la carte de la côte atlantique de l'Afrique et de l'Europe à partir de la mappemonde de Ptolémée : Giovanni Rhosos pour le Cardinal Bessarion autour de 1454. Photographie prise en 2007 à l'exposition sur "Marco Polo" à Séville, en Espagne.
Dessins et plans, Antiquités, Antiquités gallo-romaines, Cartographes, Seizième siècle, Claude Ptolémée (0100?-0170?), Gaule (58 av. J.-C.-511), Cartes anciennes, Antiquité gréco-romaine, sylvanus-aquitaine
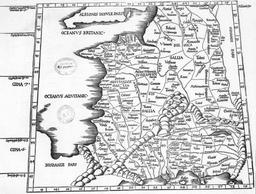
La Gaule au temps de Ptolémée
Carte de 1541 représentant les régions de Gaule au temps de Ptolémée.
Dessins et plans, Astronomie, Astronomie grecque, Claude Ptolémée (0100?-0170?), Almageste - Claude Ptolémée (0100?-0170?), Cosmogonie grecque
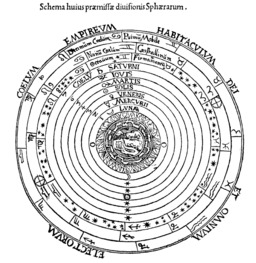
Le monde de Ptolémée
Cosmogonie de Ptolémée légendée en latin et présentant le schéma des spères concentriques : "Schema huius præmiʃʃæ diuiʃionis Sphærarum. COELVM EMPIREVM HABITACVLVM DEI ET OMNIVM ELECTORVM", notamment 7 Saturne · 6 Jupiter · 5 Mars · 4 Soleil · 3 Vénus · 2 Mercure · 1 La Lune.
Peinture, Astronomie, Astronomie de la Renaissance, Renaissance, Astronomie grecque, Claude Ptolémée (0100?-0170?), Quinzième siècle, Arts libéraux
Les arts libéraux
Représentation au XVème siècle des sept arts libéraux : Ptolémée et l'astronomie.
Dessins et plans, Antiquités, Antiquités gréco-romaines, Cartes du monde, Claude Ptolémée (0100?-0170?), Latitude, Longitude
Mappemonde de Ptolémée
Mappemonde basée sur des données de la ''Géographie'' de Ptolémée (2e siècle de notre ère) dessinée en 1544 par le cartographe bâlois Sébastien Münster, légendée en latin, avec latitudes et longitudes.
Portrait de Ptolémée
Portrait de Ptolémée, illustration de la revue "Popular science monthly" N°78 : "Genèse de la loi de la gravité" par le Pr. John C. Shedd, Avril 1911, p.316.
Gravure, Sculpture en marbre, Astronomie, Relief (sculpture), Astronomie grecque, Claude Ptolémée (0100?-0170?), Quinzième siècle, Sculpture (15e siècle), Sculpture de la Renaissance, Sculpture de portraits de la Renaissance
Ptolémée et l'Astronomie
Portrait de Ptolémée (Mathématicien, astronome, géographe, Membre présumé de l'École d'Alexandrie) vu par un artiste du XVème siècle : panneau en marbre provenant de la façade nord, registre inférieur, du campanile de Florence. Luca della Robbia (1400–1481).
Dessins et plans, Claude Ptolémée (0100?-0170?), Cartes anciennes, École d'Alexandrie (philosophie), Gaule -- Histoire
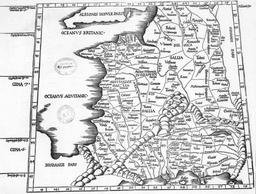
Représentation de la Gaule au temps de Ptolémée
Carte de 1541 représentant la Gaule au temps de Claude Ptolémée (0100?-0170?), mathématicien, astronome et géographe de l'école d'Alexandrie.
Gravure, Cartes du monde, Vents, Méditerranée (mer), Claude Ptolémée (0100?-0170?), Latin (langue), Cartes anciennes, Inventions, ABCD, École d'Alexandrie (philosophie), ABCD-inventions
Représentation du monde par Ptolémée
Représentation du monde et des vents légendée en latin et centrée sur la Mer Méditerranée, par Claude Ptolémée ; graveur Johannes Schnitzer. Scan d'une carte de 1482.
Dessins et plans, Géométrie, Astronomie, Claude Ptolémée (0100?-0170?), Cercles, Cercles du triangle, Mathématiciens grecs
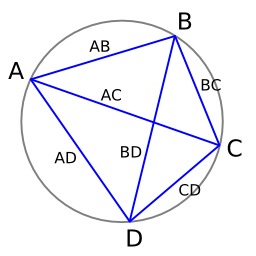
Théorème de Ptolémée
Quadrilatère illustrant le théorème de Ptolémée. Le théorème de Ptolémée est un théorème de géométrie euclidienne. Il décrit une relation algébrique entre les longueurs des côtés et des diagonales d'un quadrilatère, équivalente à l'inscription du quadrilatère dans un cercle. L'implication directe est attribuée à l'astronome et mathématicien grec Ptolémée, dont il se servit pour ses calculs liés à l'astronomie.
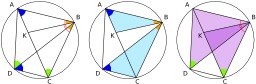
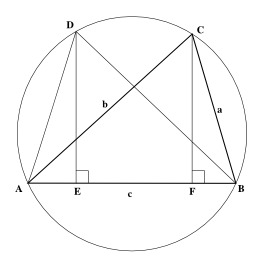
Théorème de Ptolémée
Preuve géométrique du théorème de Ptolémée. Le théorème de Ptolémée est un théorème de géométrie euclidienne. Il décrit une relation algébrique entre les longueurs des côtés et des diagonales d'un quadrilatère, équivalente à l'inscription du quadrilatère dans un cercle.
Clip art, Géométrie, Angles, Claude Ptolémée (0100?-0170?), Almageste - Claude Ptolémée (0100?-0170?)
Théorème du cosinus de Ptolémée
Au IIe siècle de notre ère, Ptolémée d’Alexandrie dans son « Almageste », a établi des égalités de rapport équivalentes aux formules d'addition et de soustraction donnant sin(A+B) et cos(A+B). Ptolémée établit une formule équivalente à la formule de l’angle moitié sin^2(A/2)=(1-cos A)/2 et dressa une table de ses résultats.