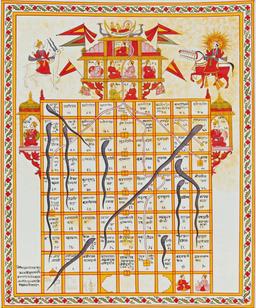
Le jeu des serpents et des échelles

Version indienne du XIXème siècle du jeu des serpents et des échelles (Gouache sur tisse). Serpents et échelles ou le jeu de l'échelle est un jeu de société populaire consistant à déplacer les jetons sur un tableau de cases avec un dé en essayant de monter les échelles et en évitant de trébucher sur les serpents. Il est suggéré que l'origine du jeu est moksha-patamu, un ancien jeu hindou remontant au deuxième siècle av. Jésus-Christ, créé par des enseignants hindous spirituels, où les serpents et échelles sont des symboles pour la moralité et spiritualité de la vie. Le jeu est une représentation d'un chemin spirituel que les humains prennent pour atteindre le ciel. Avec des bons gestes, le chemin est raccourci (ce que symbolise les échelles), tandis qu'avec le contraire, le chemin est allongé (d'où vient le symbolisme des serpents). Les différentes cultures ont perçu dans le jeu une valeur éducative et spirituelle, la raison commune pour laquelle ce jeu est surtout présenté aux enfants et adolescents. Les sanscrits avaient un jeu semblable appelé Dapasada. La forme moderne du jeu a été inventée par un Britannique appelé John Jaques qui travaillait pour la société Jaques of London. L'édition la plus connue du jeu est celle de Milton Bradley et Hasbro. La trajectoire suivie par les jetons suit habituellement celle d'un boustrophédon. La forme du jeu peut être mathématiquement représentée par une chaîne de Markov. Elwyn Berlekamp, John Horton Conway et Richard K. Guy ont écrit un livre pour montrer que ce jeu pouvait être traité comme un jeu impartial dans la théorie des jeux combinatoires.

→