Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.

Votre recherche ...

Nuage de mots clés

Dessins et plans | Musique -- Intervalles et gammes | Mathématiciens | Solfège | Son | Musique en muséologie | Philosophes grecs dans l'Antiquité | Pythagore (0580?-0500? av. J.-C.) | Accords (musique) |
Gamme pythagoricienne en solfège. Source : http://data.abuledu.org/URI/53b5280b-gamme-pythagoricienne-en-solfege

Dessins et plans, Musique -- Intervalles et gammes, Mathématiciens, Solfège, Son, Musique en muséologie, Philosophes grecs dans l'Antiquité, Pythagore (0580?-0500? av. J.-C.)

Gamme pythagoricienne en solfège

Construction de la gamme pythagoricienne en solfège, avec 12 quintes ascendantes ramenées dans la même octave. On descend chaque fois que possible d'une octave afin de rester dans la même (représentée en bleu ciel). Pythagore (0580?-0500? av. J.-C.) est un philosophe et mathématicien grec.

→

Intervalles de la gamme pythagoricienne. Source : http://data.abuledu.org/URI/53b5296f-intervalles-de-la-gamme-pythagoricienne

Dessins et plans, Musique -- Intervalles et gammes, Mathématiciens, Solfège, Son, Musique en muséologie, Philosophes grecs dans l'Antiquité, Accords (musique), Pythagore (0580?-0500? av. J.-C.)

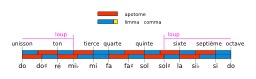
Intervalles de la gamme pythagoricienne

Représentation graphique d'une gamme pythagoricienne : il est possible de représenter une gamme pythagoricienne particulière en mettant les apotomes et les limmas les uns à la suite des autres selon les intervalles obtenus, le limma étant plus court que l'apotome d'un comma. Les deux demi-tons, qui sont identiques dans la gamme tempérée, sont nommés dans la gamme pythagoricienne : apotome, pour l'intervalle formé par une note et sa version altérée ; limma, pour l'intervalle formé par une note altérée et la note voisine ne portant pas le même nom. Ces intervalles sont disposés ainsi : do - apotome - do♯ - limma - ré, pour les quintes ascendantes ; do - limma - ré♭ - apotome - ré, pour les quintes descendantes. Dans la gamme pythagoricienne, les notes bémolisées sont inférieures d'un comma pythagoricien à leurs notes conjointes diésées, on en déduit l'ordre suivant : do - ré♭ - do♯ - ré. Source : http://fr.wikipedia.org/wiki/Accord_pythagoricien

→