Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Perspective, Architecture -- Dessins et plans, Horizon, Architecture -- Dessins et plans -- Sémiotique
Définitions de la perspective
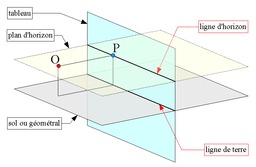
Schéma pour définir les termes principaux dans le domaine de la perspective en géométrie : Ligne de terre, Sol ou géométral, Plan d'horizon, Ligne d'horizon, Tableau.
Gravure, Géométrie, Vues, Perspective, Walter Crane (1845-1915), Perception du volume, Perception des paysages, Arts décoratifs, Tutoriels, Dessin -- Étude et enseignement
Dessin de volumes et perspective
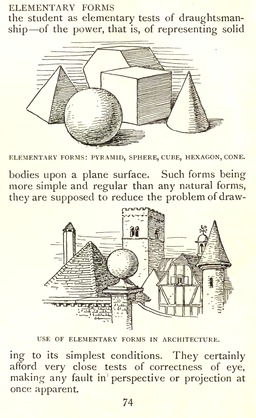
Walter Crane, Line and Form, page 74 : Dessin de volumes et respect de la perspective.
Gravure, Perspective, Dix-septième siècle, Vues perspectives, Artistes allemands, Francfort-sur-le-Main (Allemagne), Géométrie dans l'espace
Francfort
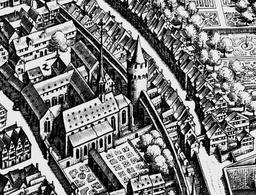
Vue de Francfort (Klostergasse, Dominikanerkloster, Staufenmauer, Mönchsturm et Judengasse), 1628, par Matthäus Merian l’Ancien (1593–1650). Les lignes parallèles dans la réalité sont représentées parallèles sur le dessin, ce qui est le propre des perspectives axonométriques, et rend mal l'effet de perspective dès que les dimensions de l'objet représenté sont importantes.
Dessins et plans, Tapisserie médiévale, Perspective, Axonométrie, Art, Arts plastiques, Bayeux (Calvados), Mathilde (prénom), Tapisserie -- France
Harold sur la Tapisserie de Bayeux
Tapisserie de Bayeux, Harold prête serment au duc Guillaume. (UBI HAROLD SACRAMENTUM FECIT WILLELMO DUCI. HIC HAROLD DUX) Source : Project Runeberg (image publiée dans la 1re (1876–1899), 2e (1904–1926) ou la 3e (1923–1937) édition du Nordisk familjebok. Les droits d'auteur sur cet ouvrage ont expiré et cette image se trouve par conséquent dans le domaine public. http://runeberg.org/nfbb/0589.html). La perspective parallèle est utilisée de manière empirique avant que ne se mettent en place les règles de perspective conique. On peut en voir des exemples dans certaines décorations de vases grecs, dans les carnets de Villard de Honnecourt., ou dans des tableaux d'Ambrogio Lorenzetti. En Orient, les peintures chinoises et japonaises ont beaucoup utilisé l'axonométrie. Cette technique permet en effet de représenter continument des évènements consécutifs et d'en rendre compte sur des rouleaux, un peu à la manière utilisée en occident pour la tapisserie de Bayeux. Elle permet aussi la représentation de scènes extrêmement étendues.
Photographie, Géométrie, Architecture des jardins, Architecture végétale des jardins, Podensac (Gironde. - région), Sauternes (Gironde), Vignobles, Géométrie de la ligne, Perspective
Jardin dans un vignoble
Photographie des jeux de ligne entre jardin et paysage du vignoble du Sauternais, entre minéral et végétal. Malle à Preignac-33.
Photographie, Sculpteurs français, Urbanisme, Perspective, Histoire, Jardins publics, Dix-neuvième siècle, Masques, Parchemin, Paris (France) -- Jardin du Luxembourg, Vues perspectives, Acteurs grecs, Bronzes français, Paris (France) -- Panthéon
Jardin du Luxembourg
Une allée du Jardin du Luxembourg. Statue en bronze de Charles-Arthur Bourgeois (1838-1886), "L'Acteur grec" : Salon de 1868. Présenté ensuite à l’Exposition universelle de 1878 où elle obtient une médaille de troisième classe. L’acteur, un masque relevé sur le front, répète son rôle en récitant son texte écrit sur un parchemin. D’abord érigé au théâtre de l’Odéon, il est réérigé au Jardin du Luxembourg : modèle du jardin public répondant aux attentes de la société française de la fin du XIXe siècle, "Voir et être vu" dans de larges allées bordées de bancs, ombragées de platanes ou de marronniers. On y accède parfois en attelage.
Lignes de perspective en peinture
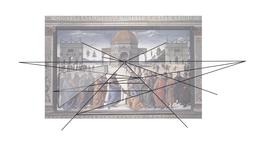
Schéma des lignes perspectives de la composition : Le Perugine, Remise des clefs à Saint Pierre (Perugino, consegna delle chiavi) 1482. Chapelle Sixtine, Rome, Vatican.
Dessins et plans, Géométrie, Perspective, Espace (architecture), Espace (art), Géométrie de l'espace, Images tridimensionnelles, Vues perspectives
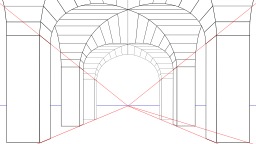
Lois de la perspective
Perspective avec lignes de fuite et point de fuite. La perspective est l'ensemble des lois permettant de représenter sur un plan des figures à trois dimensions. En art, notamment en peinture et en architecture, il faudrait parler des perspectives : diverses méthodes ont été utilisées pour donner l'illusion de la réalité tridimensionnelle.
Perspective avec projection oblique à 45°
Perspective avec projection oblique à 45°. "Malgré le nom et la description de départ sur wikimedia, cette image n'est pas un exemple de projection cavalière (la longueur des trois axes devrait être la même)".
Perspective cavalière à 90°
Comparaison entre les projections orthogonales sur les plans contenant les axes (géométrie descriptive) et la perspective cavalière : report des coordonnées. Pour effectuer une représentation en perspective cavalière, il faut choisir différents paramètres : 1) un plan frontal : un segment contenu dans ce plan, ou dans un plan parallèle, est représenté en vraie grandeur ; 2) un angle de fuite : les perpendiculaires au plan frontal, appelées fuyantes sont représentées dans cette direction ; 3) un coefficient de réduction : les longueurs représentées dans la direction de fuite sont multipliées par ce coefficient de réduction. De plus, l'alignement des points, le parallélisme des droites le rapport des longueurs de deux segments parallèles, et donc les milieux, sont conservés. En revanche, les longueurs, les aires, et les angles ne sont pas conservés dans les plans non frontaux. Les éléments cachés par les faces supposées opaques sont représentés en pointillés; les éléments visibles par l'observateur sont représentés en traits pleins.
Dessins et plans, Rues, Perspective, Architecture -- Dessins et plans, Dessin d'architecture, Dessin de bâtiment, Dessin en couleurs, Vues d'optique
Perspective et point de fuite
Dans le cadre de la représentation de la réalité en perspective conique, un point de fuite est un point imaginaire destiné à aider le dessinateur à construire son œuvre en perspective. La dénomination point de fuite est celle utilisée en dessin. Les géomètres, dans le cadre de la conception projective de l'espace dégagée à partir des propriétés des représentations en perspectives coniques, les appellent points à l'infini. À chaque direction de l'espace est associé un point de fuite.
Photographie, paris, Métros, Construction métallique, Perspective, Architecture métallique, Colonnes -- France
Perspective sous le métro aérien de Paris
Perspective sous le métro aérien à Paris (Ligne 6), entre les stations "Nationale" et "Chevaleret" (que l'on aperçoit au fond). Notez les colonnes et structures métalliques, ainsi que la voûte en brique.
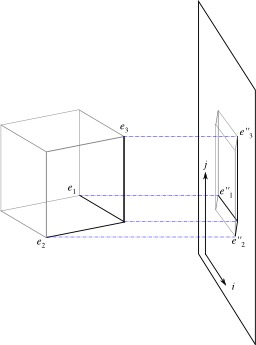
Projection orthogonale
La projection orthogonale est un type de perspective très utilisée en dessin (géométrie descriptive), et en infographie : la génération des figures est simple, par contre, on ne peut pas représenter l'éloignement (la taille des objets ne varie pas avec la distance). De manière plus générale, en algèbre linéaire, une projection orthogonale est un projecteur tel que les deux sous-espaces sont orthogonaux. La projection orthogonale permet de résoudre le problème de la plus courte distance d'un point à une droite, d'un point à un plan, ou plus généralement d'un point à un sous-espace affine d'un espace euclidien d'autre part. On peut alors utiliser ce concept pour résoudre des problèmes de type «moindres carrés». L'idée générale, basée sur le théorème de Pythagore, est que le problème de plus courte distance se ramène à une propriété d'orthogonalité.
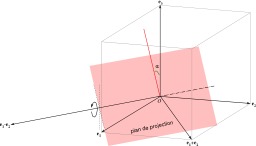
Projection orthogonale dimétrique
Projection dimétrique : le plan de projection tourne autour de la deuxième bissectrice du plan (Oxy), c'est-à-dire autour du vecteur vec{e}_1 + vec{e}_2. . Choisissons k1 = k2 ; les projections des axes x et y sont symétriques par rapport à la verticale. Cette situation est un cas particulier de la projection orthogonale avec ω = 45 °.