Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Tapisserie médiévale, Perspective, Axonométrie, Art, Arts plastiques, Bayeux (Calvados), Mathilde (prénom), Tapisserie -- France
Harold sur la Tapisserie de Bayeux
Tapisserie de Bayeux, Harold prête serment au duc Guillaume. (UBI HAROLD SACRAMENTUM FECIT WILLELMO DUCI. HIC HAROLD DUX) Source : Project Runeberg (image publiée dans la 1re (1876–1899), 2e (1904–1926) ou la 3e (1923–1937) édition du Nordisk familjebok. Les droits d'auteur sur cet ouvrage ont expiré et cette image se trouve par conséquent dans le domaine public. http://runeberg.org/nfbb/0589.html). La perspective parallèle est utilisée de manière empirique avant que ne se mettent en place les règles de perspective conique. On peut en voir des exemples dans certaines décorations de vases grecs, dans les carnets de Villard de Honnecourt., ou dans des tableaux d'Ambrogio Lorenzetti. En Orient, les peintures chinoises et japonaises ont beaucoup utilisé l'axonométrie. Cette technique permet en effet de représenter continument des évènements consécutifs et d'en rendre compte sur des rouleaux, un peu à la manière utilisée en occident pour la tapisserie de Bayeux. Elle permet aussi la représentation de scènes extrêmement étendues.
Gravure, Géométrie, Dix-huitième siècle, Savants, Savants anglais, Perspective cavalière, Axonométrie, Fortifications
Perspective cavalière en dessins de fortifications
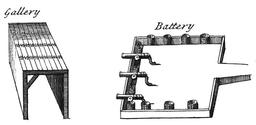
Source : Ephraim Chambers (1680–1740), "Cyclopaedia, or an Universal Dictionary of Arts and Sciences" 1728. La perspective cavalière est une manière de représenter en deux dimensions des objets en volume. Cette représentation ne présente pas de point de fuite : la taille des objets ne diminue pas lorsqu'ils s'éloignent. C'est une forme particulière de perspective axonométrique, où l'on situe les points grâce à leurs coordonnées dans un repère formé de trois axes. Dans cette perspective, deux des axes sont orthogonaux et ont un facteur de report de 1. Le troisième axe est incliné, en général de 30 ou 45° par rapport à l'horizontale, appelé « angle de fuite », et a un facteur de report inférieur à 1, en général. Cette perspective ne prétend pas donner l'illusion de ce qui peut être vu, mais simplement donner une information sur la notion de profondeur. Simple à réaliser, c'est une perspective naïve qui peut traduire un manque de « vision dans l'espace ». Trop souvent utilisée dans les dessins à main levée, elle est malgré tout à déconseiller par son ambiguïté de représentation : un objet éloigné d'un autre peut sembler être plutôt au-dessus ou au-dessous. Cette représentation était utilisée initialement pour la conception des fortifications militaires. Le « cavalier » est un promontoire de terre situé en arrière des fortifications et qui permet de voir par-dessus, et donc de voir les assaillants. La perspective cavalière était donc la vue que l'on avait du haut du cavalier (les anglais utilisent parfois le terme de « high view point », en français « point de vue de haut »). Certains avancent également que c'est la vue qu'a un cavalier du haut de son cheval.
Projection axonométrique
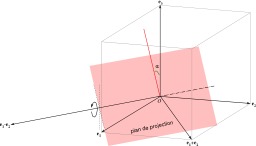
Principe de l'axonométrie : le pavé se projette sur le plan Π' selon la direction S, l'image obtenue est une perspective axonométrique du pavé.
Projection orthogonale
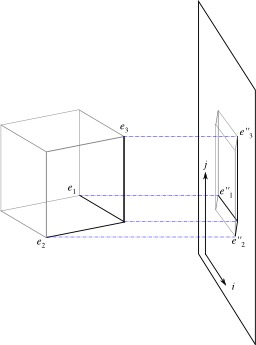
La projection orthogonale est un type de perspective très utilisée en dessin (géométrie descriptive), et en infographie : la génération des figures est simple, par contre, on ne peut pas représenter l'éloignement (la taille des objets ne varie pas avec la distance). De manière plus générale, en algèbre linéaire, une projection orthogonale est un projecteur tel que les deux sous-espaces sont orthogonaux. La projection orthogonale permet de résoudre le problème de la plus courte distance d'un point à une droite, d'un point à un plan, ou plus généralement d'un point à un sous-espace affine d'un espace euclidien d'autre part. On peut alors utiliser ce concept pour résoudre des problèmes de type «moindres carrés». L'idée générale, basée sur le théorème de Pythagore, est que le problème de plus courte distance se ramène à une propriété d'orthogonalité.
Projection orthogonale dimétrique
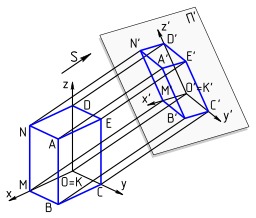
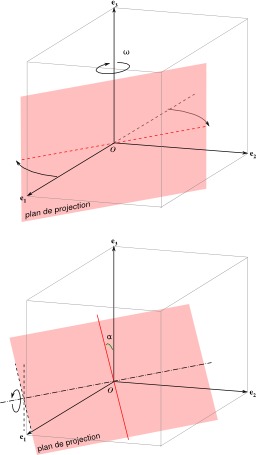
Projection dimétrique : le plan de projection tourne autour de la deuxième bissectrice du plan (Oxy), c'est-à-dire autour du vecteur vec{e}_1 + vec{e}_2. . Choisissons k1 = k2 ; les projections des axes x et y sont symétriques par rapport à la verticale. Cette situation est un cas particulier de la projection orthogonale avec ω = 45 °.
Projection orthogonale et rotation
Angles de rotation du plan de projection afin d'obtenir une perspective par projection orthogonale avec l'axe des ''z'' vertical. On peut décrire le plan de projection par des rotations transformant un plan donné, par exemple le plan (Oxz). Si l'on s'impose que la projection de vec{e}_3 reste verticale, alors on voit que le plan de projection peut s'obtenir par deux rotations, par exemple : 1) une rotation autour de l'axe (Ox) ; puis une rotation autour de la projection de (Oz) sur le plan. 2) On peut aussi procéder dans « l'ordre inverse » : une rotation autour de (Oz) ; puis une rotation autour de la trace du plan (Oxy) sur le plan de projection.
Gravure, Géométrie, Paris (France) -- Palais des Tuileries, Monuments historiques, Axonométrie, Projection axonométrique, Jacques Androuet Du Cerceau (1510?-1585?), Tuileries (Paris, France), Palais des
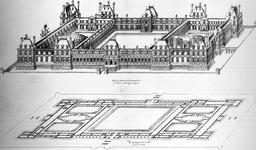
Projet du château des Tuileries
Dessin en perspective cavalière du projet de château des Tuileries, en 1578-1579, par Jacques Androuet du Cerceau (1510-1584). Les premières représentations en perspective parallèle apparaissent au XVIe siècle sous la plume d'Androuet du Cerceau qui construit des perspectives cavalières empiriques. Jacques Ier Androuet du Cerceau (1510 ? -1585 ?), est un graveur et architecte français de la seconde moitié du XVIe siècle, célèbre pour ses gravures d'architecture et ses publications : il a publié quelques livres contenant des modèles très importants d'ornements et des travaux sur l'architecture, qui auront une forte influence sur les architectes français du XVIIe siècle et au-delà. Son ouvrage le plus connu reste "Les plus excellents bastiments de France" où il décrit avec minutie et talent les réalisations majeures des architectes de son temps. Ses dessins, plans, élévations, détails et commentaires constituent un témoignage unique sur des constructions dont beaucoup n'existent plus aujourd'hui, ou ont été très largement remodelées par les siècles.