Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Musique, Partitions (musique), Solfège, Arnaud Pérat, RyXéo, Croche, Partitions -- Lecture et déchiffrage, Accord (musique), Accords (musique), Solfègse
Croche en solfège
En solfège, une croche est une figure de note représentée par un ovale de couleur noire, attaché à une hampe munie d'un crochet. La position de cet ovale sur la portée indique sa hauteur. Le crochet peut être multiplié afin de diviser la durée de la note : on construit ainsi des doubles, triples et quadruples croches. La durée d'une croche est égale à la moitié d'une noire, au quart d'une blanche, et au huitième d'une ronde. À l'inverse, elle vaut le double d'une double croche, le quadruple d'une triple croche, etc. La hampe est orientée indifféremment vers le haut ou le bas pour des raisons d'esthétique et de facilité de lecture. On l'oriente généralement vers le haut lorsque la note se situe en bas de la portée et inversement, pour limiter les débordements. Source : http://fr.wikipedia.org/wiki/Croche_%28musique%29.
Dessins et plans, Musique -- Intervalles et gammes, Mathématiciens, Solfège, Son, Musique en muséologie, Philosophes grecs dans l'Antiquité, Accords (musique), Pythagore (0580?-0500? av. J.-C.)
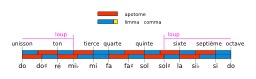
Intervalles de la gamme pythagoricienne
Représentation graphique d'une gamme pythagoricienne : il est possible de représenter une gamme pythagoricienne particulière en mettant les apotomes et les limmas les uns à la suite des autres selon les intervalles obtenus, le limma étant plus court que l'apotome d'un comma. Les deux demi-tons, qui sont identiques dans la gamme tempérée, sont nommés dans la gamme pythagoricienne : apotome, pour l'intervalle formé par une note et sa version altérée ; limma, pour l'intervalle formé par une note altérée et la note voisine ne portant pas le même nom. Ces intervalles sont disposés ainsi : do - apotome - do♯ - limma - ré, pour les quintes ascendantes ; do - limma - ré♭ - apotome - ré, pour les quintes descendantes. Dans la gamme pythagoricienne, les notes bémolisées sont inférieures d'un comma pythagoricien à leurs notes conjointes diésées, on en déduit l'ordre suivant : do - ré♭ - do♯ - ré. Source : http://fr.wikipedia.org/wiki/Accord_pythagoricien