Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, animaux prédateurs, Populations, Probabilités, Prédateurs et proies, Biologie des populations, Équations, Équations d'évolution, Équations différentielles
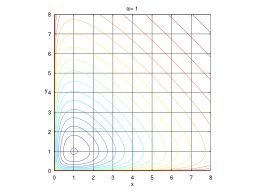
Équations proie-prédateur de Lotka-Volterra
Courbes d'évolution d'un système complexe, formé de deux espèces, proie et prédateur : équations de Lotka-Volterra. L'effectif des proies est x(t), celui des prédateurs y(t) . On retombe sur le cas précédent si y est nul. La quantité x(t)y(t) est une probabilité de rencontre, qui influe négativement sur une population (les proies), positivement sur l'autre (les prédateurs). À chaque instant, connaissant les populations en présence, on peut décrire la tendance. Ces deux équations sont couplées c'est-à-dire qu'il faut les résoudre ensemble. Mathématiquement, il faut les concevoir comme une seule équation d'inconnue le couple (x(t),y(t)) . Si l'effectif initial des populations est connu, l'évolution ultérieure est parfaitement déterminée. Elle se fait le long d'une des courbes d'évolution figurées ci-contre, qui laissent apparaître un comportement cyclique.
Dessins et plans, Géométrie, Équations, Identités remarquables, Équations -- Solutions numériques, Équations algébriques, Équations du second degré
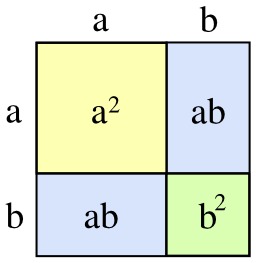
Identité remarquable du second degré
Identité remarquable du second degré : équation (a+b)^2=a^2 + 2ab + b^2. Pour se convaincre de la véracité de la formule, on considère cette figure qui représente un carré. On suppose que la longueur côté du carré jaune est égale à a et celle du carré vert à b. L'aire du grand carré est égale à (a + b)^2. Il existe une autre manière d'exprimer cette aire, elle est la somme des aires jaune, verte et des deux zones bleues. L'aire jaune est égale à a^2 car c'est un carré de côté a, l'aire verte est égale à b^2 et chaque rectangle bleu possède des côtés de longueur a et b, leur aire est égale à ab. Comme il existe deux rectangles bleus, on obtient bien la formule annoncée.