Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
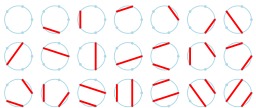
Cordes de Motzkin entre cinq points sur un cercle
Vingt-une cordes de Motzkin (qui ne se coupent pas) entre cinq points sur un cercle.
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
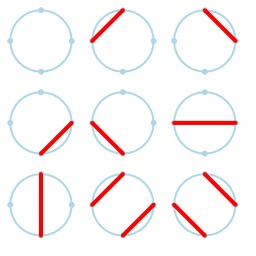
Cordes de Motzkin entre quatre points sur un cercle
Cordes de Motzkin sur un cercle : les neuf manières de dessiner des cordes qui ne se coupent pas entre quatre points d'un cercle. Le nombre de Motzkin est le nombre de façons de choisir des cordes ne se coupant pas, parmi les cordes reliant n points disposés sur un cercle. Source : http://fr.wikipedia.org/wiki/Nombre_de_Motzkin.
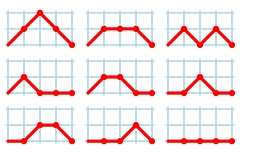
Interprétation du nombre de Motzkin pour quatre pas
Neuf chemins de Motzkin de (0, 0) à (4, 0), pour 4 pas en ne faisant que des pas Nord-Est, Est et Sud-Est. Les chemins sont en bijection avec les arbres. Source : http://fr.wikipedia.org/wiki/Nombre_de_Motzkin.