Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Abaques (mathématiques), Arithmétique, Unités arithmétiques et logiques, Cinq (le nombre), Multiplication (arithmétique), Bouliers
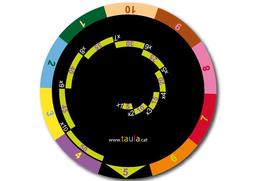
Boulier-Abaque
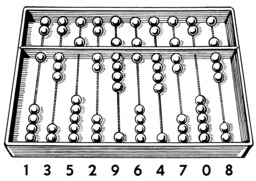
Croquis d'un abaque boulier : les unités sont placées en haut de la tige inférieure et les multiples de cinq en bas de la tige supérieure ; le nombre se lit donc au milieu du boulier ; chaque colonne peut représenter les nombres de 0 à 15 pour le report des retenues par multiples de 5. Voici le décompte de 1352964708, de gauche à droite : 1 = 1 + 0x5 ; 3 = 3 + 0x5 ; 5 = 0 + 1x5 ; 2 = 2 + 0x5 ; 9 = 4 + 1x5 ; 6 = 1 + 1x5 ; 4 = 4 + 0x5 ; 7 = 2 + 1x5 ; 0 = 0 + 0x5 ; 8 = 3 + 5x1.
Dessins et plans, rectangles, Puzzles, Multiplication (arithmétique), Pavages (mathématiques), Pentaminos
Les quatre pentaminos
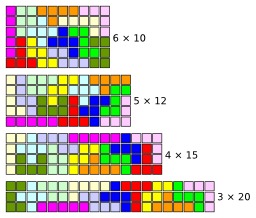
Avec les pentaminos, le puzzle classique est de paver une surface rectangulaire sans trou et ni chevauchement. Chaque pentamino, au nombre de 12, contient 5 carrés. En conséquence, le rectangle doit faire 60 carrés de surface ; les dimensions possibles sont donc 6×10, 5×12, 4×15 et 3×20. Les joueurs les plus motivés parviennent à les compléter en quelques heures à la main.
Multiplication de deux carrés magiques - 1
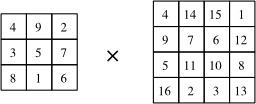
Multiplication de deux carrés magiques : Soit à effectuer le « produit » de ces deux carrés magiques, un de 3x3 et l'autre de 4x4. Le carré magique final sera de 12x12. Le « produit » de deux carrés magiques crée un carré magique d'ordre supérieur aux deux multiplicandes. Ce produit s'effectue ainsi. Soit les carrés magiques M et N : 1) Le carré final sera d'ordre MxN ; 2) Diviser le damier final en NxN sous-damiers de MxM cases ; 3) Dans le carré N, réduire de 1 la valeur de tous les nombres ; 4) Multiplier ces valeurs réduites par M × M. Les résultats sont reportés dans les cases de chaque sous-damier correspondant du carré final ; 5) Les cases du carré M sont additionnées NxN fois aux cases du damier final. Source : http://fr.wikipedia.org/wiki/Carr%C3%A9_magique_%28math%C3%A9matiques%29.
Dessins et plans, Calcul, Jeux mathématiques, Multiplication (arithmétique), Carrés magiques, Démonstration (logique)
Multiplication de deux carrés magiques - 2
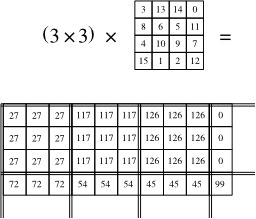
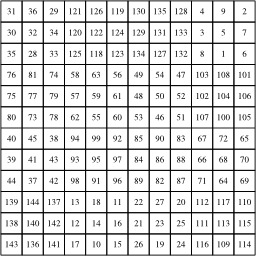
Deuxième étape de la multiplication des deux carrés magiques (3 et 4) : Le carré magique de 3x3 est remplacé par le produit (3 × 3), alors que chaque nombre du carré 4x4 est diminué de 1. Le damier final, de taille 12x12, est divisé en 4x4 sous-damiers, chacun ayant 3x3 cases. Chacune de ses cases s'obtient en multipliant (3 × 3) par l'une des cases du carré magique 4x4 « diminué ». Par exemple, 117 est le produit de 3 × 3 × 13. Ce carré est magique, mais n'est pas normal. La prochaine étape va « corriger » cette « anomalie ».
Dessins et plans, Calcul, Jeux mathématiques, Multiplication (arithmétique), Carrés magiques, Démonstration (logique)
Multiplication de deux carrés magiques - 3
Multiplication de deux carrés magiques, dernière étape : Après 4x4 additions du carré 3x3, le carré final est magique et normal.
Clip art, Arithmétique, Multiplication (arithmétique), Signes et symboles, Addition, Soustraction, Fractions, Opérations (arithmétique), Sciences -- Notation
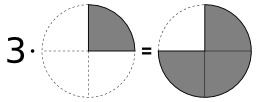
Quatre symboles arithmétiques
Quatre symboles d'opérations arithmétiques : addition (jaune), fraction (vert), soustraction (bleu) et multiplication (violet).