Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
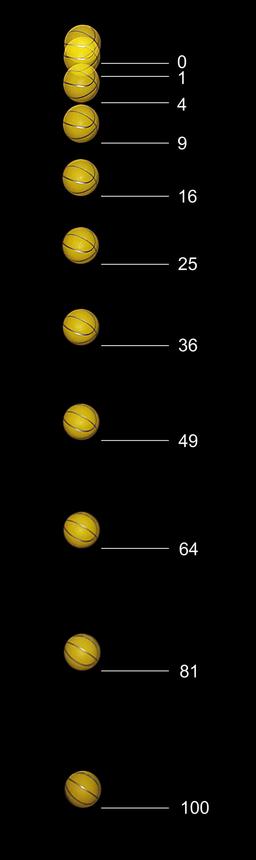
Balle en chute libre
Un objet en chute libre depuis une position fixe parcourt une distance proportionnelle au carré du temps écoulé. Cette photo a été prise sur une période de 0,5 seconde avec un flash stroboscopique réglé sur 20 impulsions par seconde. La balle, de la taille d'une balle de tennis, était retenue par un fil noir sectionné au moment où l'exposition a commencé et où le flash produisit sa première impulsion lumineuse.
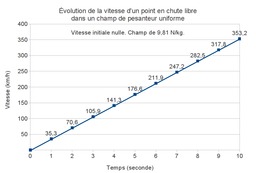
Chute libre dans un champ de pesanteur uniforme
Schéma montrant la vitesse de chute libre d'un objet en fonction du temps dans un champ de pesanteur uniforme, lorsqu'il subit l'accélération de la pesanteur de la Terre (1 g). La résistance de l'air est négligée et la vitesse initiale supposée nulle. La vitesse augmente à chaque seconde de 9,81 m/s.
Dessins et plans, Carré, Falaises, Chute libre, Formes (mathématiques), Odysseus, Onomatopées, Personnages imaginaires
Hervé le carré s'écrase au sol et s'aplatit
Hervé le carré s'écrase au sol et s'aplatit, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Énergie mécanique -- Transmission, Dix-huitième siècle, Isaac Newton (1642-1727), Galilée (1564-1642), Chute libre, Génie mécanique, Machines -- Modèles réduits
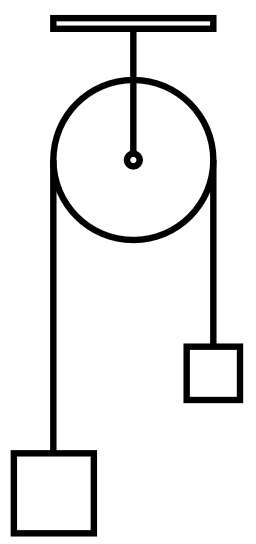
Machine d'Atwood
Machine d'Atwood (surcharge à gauche, masse à droite) : Atwood (1746-1807) est surtout célèbre chez les élèves de terminales math. élém. des années 1945-1972, par sa « machine » hautement didactique qui permettait de s'entraîner sur la bonne application de la « relation fondamentale de la dynamique » (deuxième loi de Newton) et/ou la conservation de l'énergie mécanique. Tous les grands lycées de France possèdent sans doute encore, dans leurs placards, une machine d'Atwood. Du point de vue expérimental, l'appareil fut l'objet d'un travail soutenu durant au moins un siècle, ce qui permit de tenir compte de beaucoup de correctifs. Néanmoins, pouvoir placer l'appareil dans un grand tube de Newton est resté l'apanage des très grands lycées. La chute libre est difficile à étudier quantitativement, car les temps de parcours sont très courts. Galilée est le premier à chercher comment la ralentir, sans la « dénaturer » : il pensa au plan incliné d'angle α (où intervient seulement g⋅sinα), puis à la succession de plans inclinés. La difficulté pour Galilée restait la mesure du temps… Atwood proposa « sa » machine pour diminuer l'accélération des masses.
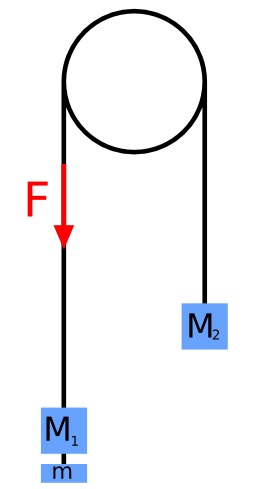
Machine d'Atwood
Machine d'Atwood : La chute libre est difficile à étudier quantitativement, car les temps de parcours sont très courts. Atwood proposa « sa » machine pour diminuer l'accélération des masses. Sur une poulie, un fil relie deux masses m_1 et m_2 (m_1 < m_2). Si les masses sont égales et le système immobile il restera ainsi en équilibre. Si l'une des masses est plus grande (m_2 > m_1, par exemple), son poids entraîne le mouvement, mais on conçoit que la masse m_1 ralentit la chute de m_2 .