Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Carré magique
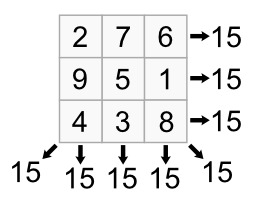
Carré magique normal d’ordre 3 et de constante magique 15. En mathématiques, un carré magique d’ordre n est composé de n^{2} nombres entiers, écrits sous la forme d’un tableau carré. Ces nombres sont disposés de sorte que leurs sommes sur chaque rangée, sur chaque colonne et sur chaque diagonale principale soient égales. On nomme alors constante magique (et parfois densité) la valeur de ces sommes.
Carré magique selon Moschopoulos
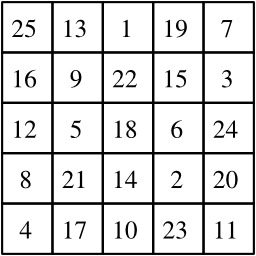
Un carré magique d'ordre 5 construit selon la méthode de Moschopoulos. La méthode de construction proposée par le Byzantin Manuel Moschopoulos, dite « parcours en cavalier d'échecs », se représente par le vecteur déplacement (1, 2) et le vecteur collision (1 + 1, 2 - 2) = (2, 0).
Dessins et plans, Arithmétique, Nombre d'or, Spirales, Mathématiques, Suite de Fibonacci, Carrés magiques
Carrés de Fibonacci en spirale
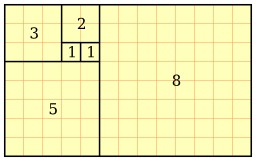
Une spirale logarithmique peut être approchée de la manière suivante : on commence à l'origine d'un repère cartésien, on se déplace de mathcal F_1 unités vers la droite, puis de mathcal F_2 unités vers le haut, on se déplace de mathcal F_3 unités vers la gauche, ensuite de mathcal F_4 unités vers le bas, puis de mathcal F_5 unités vers la droite, etc. Cela ressemble à la construction mentionnée pour le nombre d'or.
Dessins et plans, Jeux mathématiques, Mathématiciens, Carrés magiques, Claude-Gaspard Bachet (1581-1638)
Construction d'un carré magique - 1
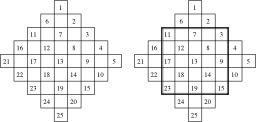
Construction d'un carré magique 5x5, méthode de Méziriac : Premières étapes de construction d'un carré magique d'ordre 5. Chaque diagonale allant de gauche à droite comporte un entier unique en ordre croissant. Ensuite, le contour du carré magique final est esquissé.
Dessins et plans, Jeux mathématiques, Mathématiciens, Carrés magiques, Claude-Gaspard Bachet (1581-1638)
Construction d'un carré magique - 2
Dernières étapes de la construction d'un carré magique 5x5 selon la méthode de Méziriac.
Dessins et plans, Calcul, Géométrie, Jeux mathématiques, Mathématiciens, Carrés magiques, John Horton Conway (1937-)
Construction d'un carré magique par la méthode du losange - 1
Premières étapes de la construction d'un carré magique 5x5 par la méthode du losange proposée par John Horton Conway : 1) Les nombres impairs 1, 3 et 5 sont inscrits selon une diagonale montante qui va de gauche à droite ; 2) Les nombres pairs 2 et 4 sont ensuite inscrits pour compléter la diagonale brisée ; 3) « Descendre » à la prochaine diagonale ; 4) Recommencer avec les nombres suivants.
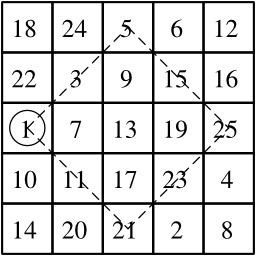
Construction d'un carré magique par la méthode du losange - 2
Un carré magique 5x5 construit selon la méthode du losange proposée par John Horton Conway : Le résultat final est un carré magique dont la constante est 65.
Dessins et plans, Jeux mathématiques, Mathématiciens, Carrés magiques, Siam, Simon de La Loubère (1643-1729)
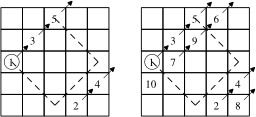
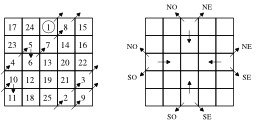
Construction d'un carré magique selon la méthode siamoise
Un carré magique d'ordre 5 avec un carré adjacent montrant des directions : construction d'un carré magique d'ordre impair selon la méthode siamoise. Dans cet exemple, le carré est rempli selon les diagonales nord-est (NE), mais elles pourraient être parallèles à sud-est (SE), à sud-ouest (SO) ou à nord-ouest (NO). 1) Placer le 1 tel que montré. 2) Décaler d'une case vers la droite puis d'une case vers le haut pour le 2, et ainsi de suite pour le 3, puis le 4, etc. 3) Si la pointe de la flèche sort du carré, revenir de l'autre côté, comme si le carré était enroulé sur un tore. 4) Si la prochaine case est occupée, décaler d'une case vers le bas. La méthode siamoise a été introduite en France par Simon de La Loubère en 1688 alors qu'il revenait de son ambassade au Siam. Source : http://fr.wikipedia.org/wiki/Carr%C3%A9_magique_%28math%C3%A9matiques%29.
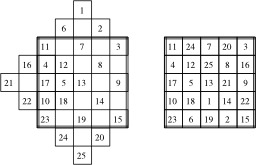
Construction de carrés magiques, nombres pairs
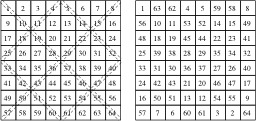
Construction d'un carré magique 8x8 selon la méthode des permutations relativement aux diagonales des sous-damiers 4x4. Dans le carré de gauche, les nombres naturels sont inscrits dans l'ordre. De plus, les diagonales principales de chaque sous-damier 4x4 sont recouvertes de lignes en pointillés. À droite, le carré final, magique, est inscrit. Chaque nombre qui n'était pas recouvert par une ligne en pointillés a été remplacé par son complément à (82 + 1) = 65.
Gravure, Géométrie, Albrecht Dürer (1471-1528), Symbolisme dans l'art, Carrés magiques, Attributs (symbolisme), Mélancolie
Mélancolie
Melencolia ou La Melencolia est le nom donné à une gravure sur cuivre d'Albrecht Dürer datée de 1514. Le titre est pris de l'œuvre où il apparaît comme un élément de la composition. Melencolia I est souvent considéré comme faisant partie d'une série, Meisterstiche, comprenant également Le chevalier, la mort et le diable (1513) et Saint Jérôme dans sa cellule (1514). Cette œuvre d'une richesse symbolique exceptionnelle a été l'objet d'un nombre considérable d'études. Source : http://fr.wikipedia.org/wiki/Melencolia_I.
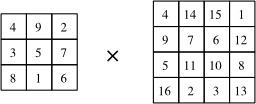
Multiplication de deux carrés magiques - 1
Multiplication de deux carrés magiques : Soit à effectuer le « produit » de ces deux carrés magiques, un de 3x3 et l'autre de 4x4. Le carré magique final sera de 12x12. Le « produit » de deux carrés magiques crée un carré magique d'ordre supérieur aux deux multiplicandes. Ce produit s'effectue ainsi. Soit les carrés magiques M et N : 1) Le carré final sera d'ordre MxN ; 2) Diviser le damier final en NxN sous-damiers de MxM cases ; 3) Dans le carré N, réduire de 1 la valeur de tous les nombres ; 4) Multiplier ces valeurs réduites par M × M. Les résultats sont reportés dans les cases de chaque sous-damier correspondant du carré final ; 5) Les cases du carré M sont additionnées NxN fois aux cases du damier final. Source : http://fr.wikipedia.org/wiki/Carr%C3%A9_magique_%28math%C3%A9matiques%29.
Dessins et plans, Calcul, Jeux mathématiques, Multiplication (arithmétique), Carrés magiques, Démonstration (logique)
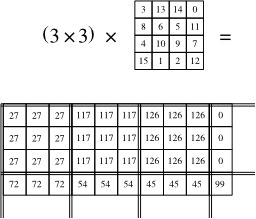
Multiplication de deux carrés magiques - 2
Deuxième étape de la multiplication des deux carrés magiques (3 et 4) : Le carré magique de 3x3 est remplacé par le produit (3 × 3), alors que chaque nombre du carré 4x4 est diminué de 1. Le damier final, de taille 12x12, est divisé en 4x4 sous-damiers, chacun ayant 3x3 cases. Chacune de ses cases s'obtient en multipliant (3 × 3) par l'une des cases du carré magique 4x4 « diminué ». Par exemple, 117 est le produit de 3 × 3 × 13. Ce carré est magique, mais n'est pas normal. La prochaine étape va « corriger » cette « anomalie ».
Dessins et plans, Calcul, Jeux mathématiques, Multiplication (arithmétique), Carrés magiques, Démonstration (logique)
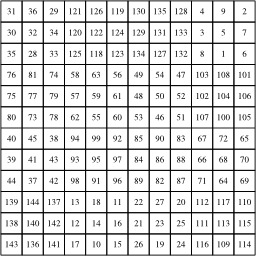
Multiplication de deux carrés magiques - 3
Multiplication de deux carrés magiques, dernière étape : Après 4x4 additions du carré 3x3, le carré final est magique et normal.