Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
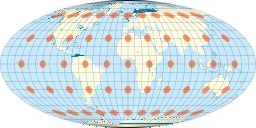
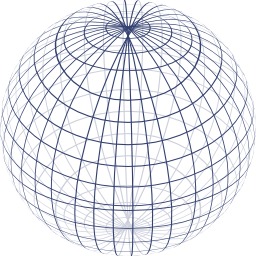
Indicatrices de Tissot sur le planisphère de Mollweide
Indicatrices de Tissot sur le planisphère de Mollweide. Chaque cercle rouge a un rayon de 500 km. Échelle : 1:5,000,000. La projection de Mollweide est une projection cartographique pseudo-cylindrique employée le plus souvent pour les planisphères de la Terre (ou du ciel). Connue aussi sous le nom de projection de Babinet ou projection elliptique, le qualificatif de projection équivalente de Mollweide indique qu'elle privilégie la conservation des surfaces à la conservation des angles (projection conforme) : c'est pourquoi on y recourt principalement pour les cartes de l'ensemble de la sphère reproduites sur une surface réduite. Cette projection fut publiée pour la première fois en 1805 par le mathématicien et astronome prussien Karl (ou Carl) Brandan Mollweide (1774 – 1825) de Leipzig, en tant qu’alternative à la projection de Mercator. Jacques Babinet en vulgarisa l’emploi en 1857, sous le nom de projection homolographique.
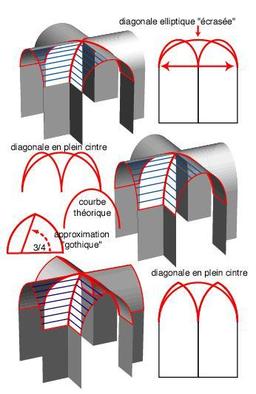
Croisée d'ogives
Genèse de la croisée d'ogives. La projection orthogonale de cette croisée selon l’axe de chacune des nefs donne une demi-ellipse posée dans sa hauteur, très résistante en son sommet. Par chance, il existe une bonne approximation de cet arc pour cette époque où, sur le chantier, à défaut de bons moyens de calcul et de mesures précises il vaut mieux recourir à des tracés simples à exécuter : il s’agit d'un arc brisé composé de deux arcs de cercle centrés respectivement au premier et au troisième quart de la distance à franchir. Cette approximation est souvent observable à une légère déformation de la voûte de la croisée à l'endroit où elle se raccorde aux nefs.
Dessins et plans, Géométrie, Cauchy (Augustin Louis, baron), 1789-1857, Dodécaèdres, Polyèdres, Projection stéréographique
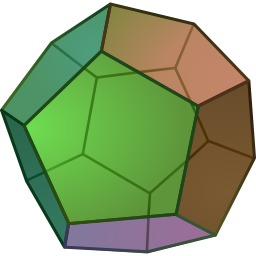
Dodécaèdre
Le dodécaèdre, un polyèdre régulier convexe. En 1811, Cauchy (1789-1857) s’intéresse dans son premier mémoire à l’égalité de polyèdres convexes dont les faces sont égales. Il propose une démonstration du théorème de Descartes-Euler, concernant les nombres de sommets, de faces et d'arêtes d'un polyèdre convexe. Sa preuve consiste à projeter le polyèdre en un graphe planaire suivant ce qui est aujourd’hui appelé une projection stéréographique. Cependant, Cauchy commit une erreur, en ne faisant pas d’hypothèse claire sur les polyèdres étudiés. Dans son second mémoire en 1812, il donna des formules pour calculer les angles diédraux.
Perspective avec projection oblique à 45°
Perspective avec projection oblique à 45°. "Malgré le nom et la description de départ sur wikimedia, cette image n'est pas un exemple de projection cavalière (la longueur des trois axes devrait être la même)".
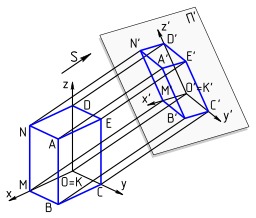
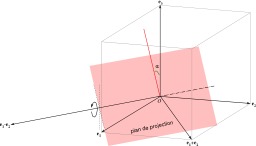
Projection axonométrique
Principe de l'axonométrie : le pavé se projette sur le plan Π' selon la direction S, l'image obtenue est une perspective axonométrique du pavé.
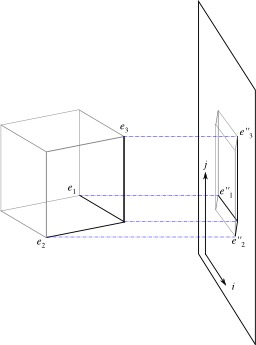
Projection orthogonale
La projection orthogonale est un type de perspective très utilisée en dessin (géométrie descriptive), et en infographie : la génération des figures est simple, par contre, on ne peut pas représenter l'éloignement (la taille des objets ne varie pas avec la distance). De manière plus générale, en algèbre linéaire, une projection orthogonale est un projecteur tel que les deux sous-espaces sont orthogonaux. La projection orthogonale permet de résoudre le problème de la plus courte distance d'un point à une droite, d'un point à un plan, ou plus généralement d'un point à un sous-espace affine d'un espace euclidien d'autre part. On peut alors utiliser ce concept pour résoudre des problèmes de type «moindres carrés». L'idée générale, basée sur le théorème de Pythagore, est que le problème de plus courte distance se ramène à une propriété d'orthogonalité.
Projection orthogonale dimétrique
Projection dimétrique : le plan de projection tourne autour de la deuxième bissectrice du plan (Oxy), c'est-à-dire autour du vecteur vec{e}_1 + vec{e}_2. . Choisissons k1 = k2 ; les projections des axes x et y sont symétriques par rapport à la verticale. Cette situation est un cas particulier de la projection orthogonale avec ω = 45 °.
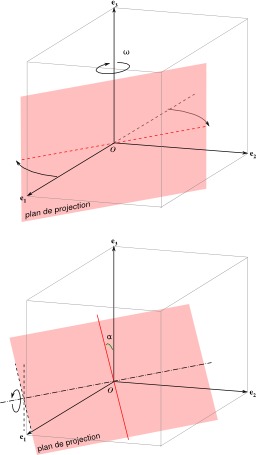
Projection orthogonale et rotation
Angles de rotation du plan de projection afin d'obtenir une perspective par projection orthogonale avec l'axe des ''z'' vertical. On peut décrire le plan de projection par des rotations transformant un plan donné, par exemple le plan (Oxz). Si l'on s'impose que la projection de vec{e}_3 reste verticale, alors on voit que le plan de projection peut s'obtenir par deux rotations, par exemple : 1) une rotation autour de l'axe (Ox) ; puis une rotation autour de la projection de (Oz) sur le plan. 2) On peut aussi procéder dans « l'ordre inverse » : une rotation autour de (Oz) ; puis une rotation autour de la trace du plan (Oxy) sur le plan de projection.
Gravure, Géométrie, Paris (France) -- Palais des Tuileries, Monuments historiques, Axonométrie, Projection axonométrique, Jacques Androuet Du Cerceau (1510?-1585?), Tuileries (Paris, France), Palais des
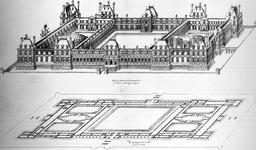
Projet du château des Tuileries
Dessin en perspective cavalière du projet de château des Tuileries, en 1578-1579, par Jacques Androuet du Cerceau (1510-1584). Les premières représentations en perspective parallèle apparaissent au XVIe siècle sous la plume d'Androuet du Cerceau qui construit des perspectives cavalières empiriques. Jacques Ier Androuet du Cerceau (1510 ? -1585 ?), est un graveur et architecte français de la seconde moitié du XVIe siècle, célèbre pour ses gravures d'architecture et ses publications : il a publié quelques livres contenant des modèles très importants d'ornements et des travaux sur l'architecture, qui auront une forte influence sur les architectes français du XVIIe siècle et au-delà. Son ouvrage le plus connu reste "Les plus excellents bastiments de France" où il décrit avec minutie et talent les réalisations majeures des architectes de son temps. Ses dessins, plans, élévations, détails et commentaires constituent un témoignage unique sur des constructions dont beaucoup n'existent plus aujourd'hui, ou ont été très largement remodelées par les siècles.