Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Arbres (théorie des graphes), Arbres (théorie des graphes) -- Informatique, Calcul sur des intervalles, Graphes d'intersections, Théorie des, Graphes, Théorie des
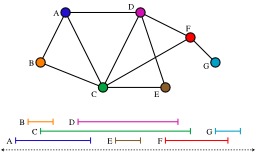
Graphe d'intervalle
Sept intervalles de la droite réelle et le graphe d'intervalle associé : en théorie des graphes, un graphe d'intervalle est le graphe d'intersection (en) d'un ensemble d'intervalles de la droite réelle. Chaque sommet du graphe d'intervalle représente un intervalle de l'ensemble et une arête relie deux sommets à l'intersection des deux intervalles correspondants. Les graphes d'intervalle sont utilisés pour modéliser les problèmes d'allocation de ressources en recherche opérationnelle. Chaque intervalle représente l'allocation d'une ressource pendant un certain temps; la recherche du stable maximum du graphe correspond à la meilleure allocation de ressources pouvant être réalisée sans conflits. La recherche d'un ensemble d'intervalles qui représente un graphe d'intervalle peut aussi être une manière d'assembler des séquences contigües d'ADN.
Dessins et plans, Ponts, Graphes, Théorie des, Cartes géographiques, Leonhard Euler (1707-1783), Plans de villes, Königsberg (Russie), Ponts (théorie des graphes)
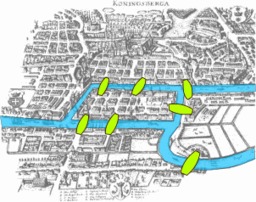
Les ponts de Konigsberg
Représentation graphique du problème des sept ponts de Königsberg. Leonhard Euler (1707-1783) est un mathématicien et physicien suisse, qui fit d'importantes découvertes dans des domaines aussi variés que le calcul infinitésimal et la théorie des graphes.