Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres non-rationnels, Nombres transcendants, Pi (le nombre)
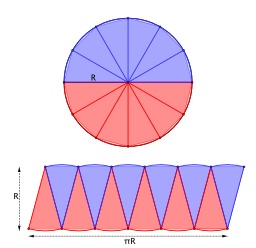
Calcul de l'aire du cercle avec Géogébra
Calcul de l'aire du cercle avec Géogébra : rayon x demi-circonférence. On déduit d’une propriété analogue pour les polygones réguliers que l’aire d’un cercle égale son demi-périmètre multiplié par son rayon. le périmètre du polygone est à peu près 2πr alors qu’en redistribuant les triangles formés on remarque que son aire est à peu près πr2. Pour formaliser le « à peu près » il faudrait faire tendre le nombre de côtés du polygone vers l’infini, ce qui illustre déjà la nature « analytique » de π.
Dessins et plans, Cube, Carré, Géométrie des nombres, Gnomonique, Abu Bakr Muhammad ibn al-Hasan al- Karaji (....-1019 ?)
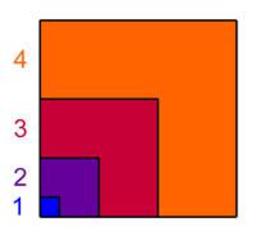
Carré d'un nombre triangulaire
Démonstration géométrique de la formule donnant le carré d'un nombre triangulaire, égal à la somme des premiers cubes parfaits : le carré du nième nombre triangulaire est égal à la somme des n premiers cubes. L'illustration géométrique permet de se convaincre de la véracité de ses propositions. L'aire de la zone orange de la figure est appelée nombre gnomonique. Elle est constituée de deux rectangles de base 4 et de côté le nombre triangulaire d'indice 4, c'est-à-dire 10. Ces deux rectangles se recoupent sur un carré de côté 4, on en déduit que l'aire orange est égale à 5 x 4 x 4 - 4 x 4, ou encore 43. Ce raisonnement est valable sur chaque nombre gnomonique, l'aire du carré de côté le nombre triangulaire d'indice 4 est égal la somme des 4 premiers cubes. De cette démonstration d'Al-Karaji, on déduit la première proposition.
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres transcendants, Pi (le nombre)
Encadrement de PI par Liu Hui
Représentation de l'encadrement de π par Liu Hui. Si les calculs pratiques peuvent se faire avec une bonne précision en utilisant la valeur 3,14 comme approximation de π, la curiosité des mathématiciens les pousse à déterminer ce nombre avec plus de précision. Au IIIe siècle, en Chine, Liu Hui, commentateur des Neuf chapitres, propose comme rapport entre le périmètre et le diamètre la valeur pratique de 3 mais développe des calculs proches de ceux d’Archimède mais plus performants et fournit une approximation de π de 3,1416.
Nombre pyramidal carré 30
Représentation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16.
Nombres triangulaires
Somme de quatre nombres triangulaires (pair) : le nombre triangulaire d'indice n est somme de quatre nombres triangulaires. Ceci est vrai quelle que soit la parité de l'indice n. En effet, u14 est la somme de trois fois u7 et de u6 et u15 est la somme trois fois u7 et de u8.
Dessins et plans, Nombres cardinaux, Chiffres, Imagerie (psychologie), Images mentales, Jeux arithmétiques, Géométrie des nombres
Représentations linéaires de nombres
Plusieurs exemples de représentations linéaires de nombres, 1892-1893. Source : Popular Science Monthly, Volume 42, "Number forms", par G. T. W. Patrick, professeur de philosophie à l'université d'Iowa.
Somme de huit nombres triangulaires
La somme de huit fois un nombre triangulaire et de un est un carré parfait.
Dessins et plans, Carré, Surfaces (mathématiques) -- Volumes, Géométrie des nombres, Johann Faulhaber (1580-1635), Pyramides (géométrie)
Somme des carrés
Un exemple de preuve sans mots à propos de la somme des premiers carrés : chacune des trois pyramides a pour volume la somme des carrés de 1 à n (n=4 dans cette illustration) ; le parallélépipède final est de côtés n, n+1 et n+1/2. Ce résultat se généralise pour la somme des n premières puissances strictement positives. Cette somme porte le nom de formule de Faulhaber. Johann Faulhaber (1580-1635) est un mathématicien allemand qui collabora avec Kepler.
Dessins et plans, Géométrie, Aires (surfaces), Aires (surfaces) -- Mesure, Nombres transcendants, Pi (le nombre), British library -- Manuscrits. Papyrus 10188, Papyrus Bremner-Rhind
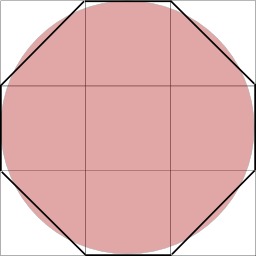
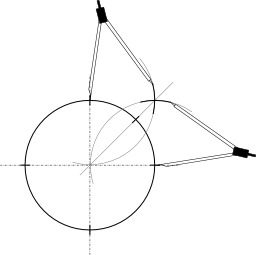
Approximation de PI par Ahmès
Illustration de l'approximation de π (PI) par Ahmès (Égypte). Découvert en 1855, le papyrus de Rhind contient le texte, recopié vers l’an 1650 avant notre ère par le scribe égyptien Ahmès, d’un manuel de problèmes pédagogiques très ancien. On y trouve une méthode pour évaluer l’aire d’un disque en prenant le carré dont le côté est égal au diamètre du disque diminué d’un neuvième. Cette méthode conduit à une évaluation de π de 256/81. Dans l’illustration ci-contre, le disque a pour diamètre 9. L’aire du disque est légèrement supérieure à l’aire de l’octogone irrégulier obtenu en rognant les coins du carré de côté 9. Cet octogone a pour aire 63, l’aire du disque est alors évaluée à 64 soit l’aire d’un carré de côté 8. Le rapport entre l’aire du disque et le carré du rayon est alors évalué par 64/(9/2)^2, c’est-à-dire 256/81.
Dessins et plans, Calcul, Géométrie, Jeux mathématiques, Mathématiciens, Carrés magiques, John Horton Conway (1937-)
Construction d'un carré magique par la méthode du losange - 1
Premières étapes de la construction d'un carré magique 5x5 par la méthode du losange proposée par John Horton Conway : 1) Les nombres impairs 1, 3 et 5 sont inscrits selon une diagonale montante qui va de gauche à droite ; 2) Les nombres pairs 2 et 4 sont ensuite inscrits pour compléter la diagonale brisée ; 3) « Descendre » à la prochaine diagonale ; 4) Recommencer avec les nombres suivants.
Dessins et plans, Géométrie, Drapeaux, Douze (le nombre), Pays de l'Union européenne, Histoire, Europe
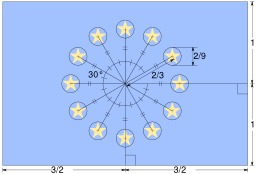
Construction géométrique du drapeau de l'Europe
Construction géométrique du drapeau de l'Europe : Le drapeau est rectangulaire avec une proportion de 2:3. Il est composé d'un cercle de douze étoiles d'or sur un champ d'azur. Toutes les étoiles sont disposées verticalement (la pointe vers le haut), ont cinq branches et sont espacées de façon égale selon les positions des heures sur cadran d'une horloge. Chaque rayon d'étoile est égal à un dix-huitième de la hauteur du guindant. La description héraldique officielle donnée par l'Union européenne est : « Le drapeau européen est représenté par un cercle de douze étoiles d'or sur fond bleu. Les étoiles symbolisent les idéaux d'unité, de solidarité et d'harmonie entre les peuples d'Europe. »
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
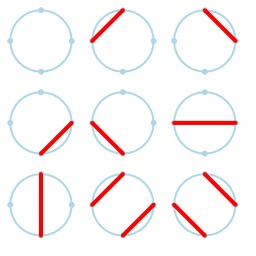
Cordes de Motzkin entre quatre points sur un cercle
Cordes de Motzkin sur un cercle : les neuf manières de dessiner des cordes qui ne se coupent pas entre quatre points d'un cercle. Le nombre de Motzkin est le nombre de façons de choisir des cordes ne se coupant pas, parmi les cordes reliant n points disposés sur un cercle. Source : http://fr.wikipedia.org/wiki/Nombre_de_Motzkin.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas, Compas,
Couper un cercle en 8
Le tracé d'une bissectrice permet de définir deux arcs égaux, et ici de diviser le cercle en 8 parties égales : placer un point entre chaque point déjà placé : on place la pointe du compas sur un des points et l'on trace un arc de cercle à l'extérieur du cercle de base, et l'on fait de même sur le point voisin ; l'intersection des deux arcs définit un point. Puis, on trace à la règle le diamètre passant par ce point-là ; il coupe l'arc de cercle en deux parts égales (bissectrice de l'angle). Ainsi, si le cercle est déjà coupé en 4 parts, on en obtient 8 ; si le cercle est déjà coupé en 12 parts, on en obtient 24. On peut recouper les arcs en 2 par la même méthode, et multiplier ainsi le nombre d'arcs par 2, pour obtenir encore plus d'arcs.
Dessins et plans, Géométrie, Cauchy (Augustin Louis, baron), 1789-1857, Dodécaèdres, Polyèdres, Projection stéréographique
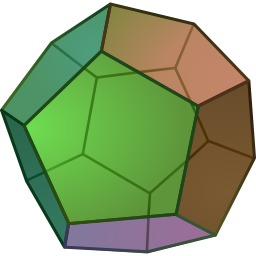
Dodécaèdre
Le dodécaèdre, un polyèdre régulier convexe. En 1811, Cauchy (1789-1857) s’intéresse dans son premier mémoire à l’égalité de polyèdres convexes dont les faces sont égales. Il propose une démonstration du théorème de Descartes-Euler, concernant les nombres de sommets, de faces et d'arêtes d'un polyèdre convexe. Sa preuve consiste à projeter le polyèdre en un graphe planaire suivant ce qui est aujourd’hui appelé une projection stéréographique. Cependant, Cauchy commit une erreur, en ne faisant pas d’hypothèse claire sur les polyèdres étudiés. Dans son second mémoire en 1812, il donna des formules pour calculer les angles diédraux.
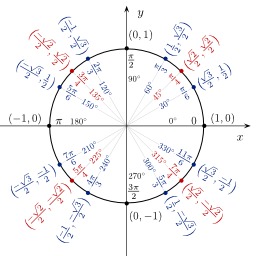
Fonctions trigonométriques dans le cercle unité
Représentation des fonctions trigonométriques dans le cercle unité. Le cercle trigonométrique, en revanche, permet la définition des fonctions trigonométriques pour tous les réels positifs ou négatifs, pas seulement pour des angles de mesure en radians comprise entre 0 et π/2. Sur ce cercle sont représentés certains angles communs, et sont indiquées leurs mesures en radians figurant dans l'intervalle [–2π, 2π], soit deux mesures par angle et même trois pour l'angle nul. Notez que les angles positifs sont dans le sens trigonométrique, contraire à celui des aiguilles d'une horloge, et les angles négatifs dans le sens horaire. Une demi-droite qui fait un angle θ avec la demi-droite positive Ox de l'axe des abscisses coupe le cercle en un point de coordonnées (cos θ, sin θ). Géométriquement, cela provient du fait que l'hypoténuse du triangle rectangle ayant pour sommets les points de coordonnées (0, 0), (cos θ, 0) et (cos θ, sin θ) est égale au rayon du cercle donc à 1. Le cercle unité peut être considéré comme une façon de regarder un nombre infini de triangles obtenus en changeant les longueurs des côtés opposés et adjacents mais en gardant la longueur de leur hypoténuse égale à 1. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
Dessins et plans, Mécanique, Physique, Génie mécanique, Amortissement (mécanique), Analyse mécanique dynamique, Construction mécanique, Contact de roulement, Mécanique appliquée, Mécanique du contact
Force appliquée sous forme annulaire
Mécanique : force appliquée selon une forme annulaire. La modélisation des liaisons mécaniques s'appuie d'abord sur l'analyse de la géométrie de contact entre deux pièces. Dans un premier temps, lorsque les géométries sont considérées parfaites, on obtient un premier modèle présentant un certain nombre de degré de liaison ; ce modèle suppose un ajustement « glissant sans jeu », la liaison modélisée est dite « idéale ». Si l'on est en présence d'un jeu plus important, certains degrés de liaison disparaissent. Cela revient à considérer que les pièces flottent dans cet espace rendu disponible par le jeu. Si l'on veut modéliser correctement le comportement du système, il faut alors utiliser une autre liaison idéale que celle obtenue par l'analyse initiale. En particulier, pour avoir des machines performantes, il faut s'assurer que le mécanisme est conçu pour assurer aux pièces des positions exploitant ces jeux (alignements corrects). Ainsi, une liaison obtenue par emboîtement, sans jeu, deux cylindres complémentaires parfaits, constitue une liaison pivot glissant ; on parle de « centrage long ». Si on ajoute un jeu radial à cet ajustement, et qu'on diminue la longueur de portée, alors les deux cylindres peuvent se déplacer latéralement (mais cela reste imperceptible) et obliquer par rapport à la direction de l'axe. La liaison idéale qu'il faut utiliser pour modéliser l'assemblage est alors la liaison linéaire annulaire, et l'on parle de « centrage court ».
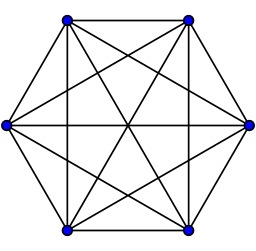
Graphe à six côtés
En théorie des graphes, le graphe complet K_n est l'unique graphe à isomorphisme près possédant n sommets tous reliés deux à deux par une arête, ici 6.
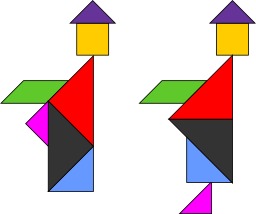
Le tangram des deux moines
Tangram du paradoxe des deux moines : même nombre de pièces mais disposées différemment.
Dessins et plans, Géométrie, Lune, Étoiles, Cinq (le nombre), Triangle, Polygones, Quatre (le nombre), Turquie
Lune et quatre étoiles turques
Reprise géométrique d'Ay yildiz, le drapeau de la Turquie : lune décroissante et étoile à cinq banches
Gravure, Géométrie, Albrecht Dürer (1471-1528), Symbolisme dans l'art, Carrés magiques, Attributs (symbolisme), Mélancolie
Mélancolie
Melencolia ou La Melencolia est le nom donné à une gravure sur cuivre d'Albrecht Dürer datée de 1514. Le titre est pris de l'œuvre où il apparaît comme un élément de la composition. Melencolia I est souvent considéré comme faisant partie d'une série, Meisterstiche, comprenant également Le chevalier, la mort et le diable (1513) et Saint Jérôme dans sa cellule (1514). Cette œuvre d'une richesse symbolique exceptionnelle a été l'objet d'un nombre considérable d'études. Source : http://fr.wikipedia.org/wiki/Melencolia_I.
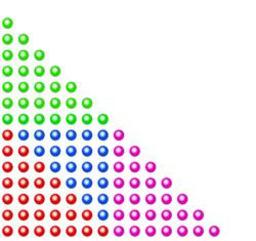
Nombre triangulaire
Le 28 est le septième nombre triangulaire ou encore le nombre triangulaire d'indice 7 : en arithmétique, un nombre triangulaire est un cas particulier de nombre figuré. Il correspond à un nombre entier positif égal au nombre de pastilles dans un triangle construit à la manière de cette figure. Source : p. 320, Die Gartenlaube (1887), Ernst Keil's Nachfolger.
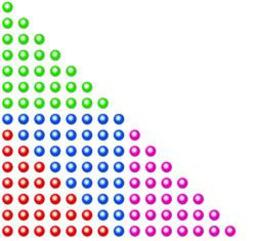
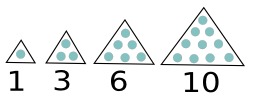
Nombres triangulaires
Représentation graphique des premiers nombres triangulaires : la représentation figurée permet un calcul pour les premières valeurs. Une définition formelle s'obtient par récurrence : le nombre triangulaire d'indice 1 est égal à 1, et un nombre triangulaire est égal à son prédécesseur additionné de son indice. Les premiers nombres triangulaires sont : 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 ... Il existe différentes manières de calculer le nombre triangulaire d'indice n, l'une d'elles est graphique et s'obtient par un raisonnement d'arithmétique géométrique.
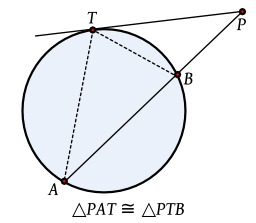
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
Puissance d'un point
En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
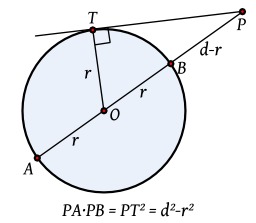
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
Puissance d'un point
Détermination de la valeur algébrique de la puissance d'un point extérieur à un cercle. En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Quarante-et-un points violets en cercles
Quarante-et-un points violets en trois cercles concentriques autour d'un point central : petit cercle de huit points et deux grands cercles de seize points.
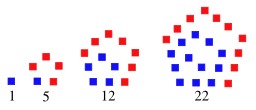
Dessins et plans, Géométrie, Douze (le nombre), Cinq (le nombre), Mathématiciens, Polygones, Numération, Un (le nombre), Léonard Euler (1707-1783), Vingt-deux (le nombre)
Quatre nombres pentagonaux
Un nombre pentagonal est un nombre figuré qui peut être représenté par un pentagone. Les premiers nombres pentagonaux sont : 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001. Les nombres pentagonaux sont importants dans la théorie des partages d'entiers d'Euler, et ils interviennent par exemple dans son théorème des nombres pentagonaux. Source : http://fr.wikipedia.org/wiki/Nombre_pentagonal
Dessins et plans, Géométrie, Cube, Jeux mathématiques, Origami, Pliages en papier, Racines numériques, Racines d'un nombre
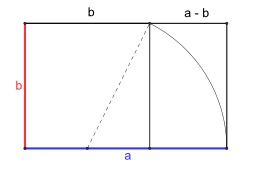
Racine cubique de 2 et origami
Doubler le volume d'un cube : PB/PA = racine cubique de 2. Comment construire la racine cubique de 2 par pliage d'origami : construction par Peter Messer, Problème 1054, Crux Mathematicorum, Vol. 12, No. 10, 1986, pp. 284-285.
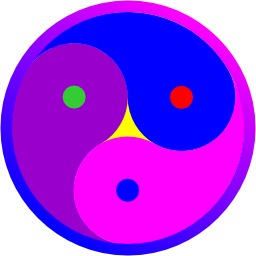
Symbole du Yin-Yang-Yuan
Le tàijí tú : symbole de la dualité yīn-yáng ; ici complémentarité à trois.
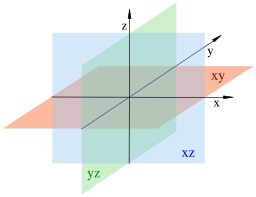
Système de coordonnées dans l'espace
En géométrie analytique, tout point du plan ou de l'espace est « repéré », c'est-à-dire qu'on lui associe un couple (dans le plan) ou un triplet (dans l'espace) de nombres.
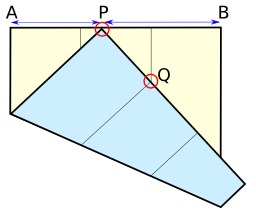
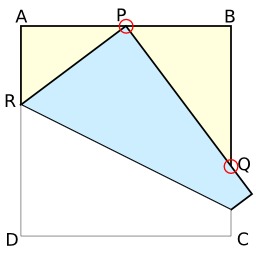
Dessins et plans, Géométrie, Carré, Jeux mathématiques, Origami, Pliages en papier, Théorèmes -- Démonstration automatique, Mathématiques japonaises, Nombres rationnels
Théorème de Haga et origami
Théorème de Haga et origami : BQ est rationnel si AP l'est, par pliage du sommet d'un carré sur un point P du côté opposé. Source : http://en.wikipedia.org/wiki/Mathematics_of_origami.