Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
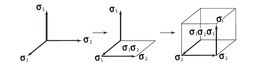
Éléments de l'algèbre géométrique
Interprétation des divers éléments d'une algèbre géométrique issue de l'espace vectoriel Euclidien 3D.
Dessins et plans, Géométrie, Équations, Identités remarquables, Équations -- Solutions numériques, Équations algébriques, Équations du second degré
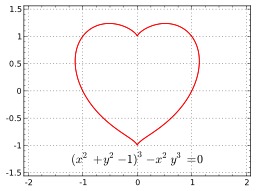
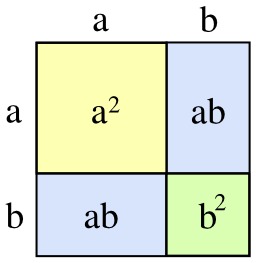
Identité remarquable du second degré
Identité remarquable du second degré : équation (a+b)^2=a^2 + 2ab + b^2. Pour se convaincre de la véracité de la formule, on considère cette figure qui représente un carré. On suppose que la longueur côté du carré jaune est égale à a et celle du carré vert à b. L'aire du grand carré est égale à (a + b)^2. Il existe une autre manière d'exprimer cette aire, elle est la somme des aires jaune, verte et des deux zones bleues. L'aire jaune est égale à a^2 car c'est un carré de côté a, l'aire verte est égale à b^2 et chaque rectangle bleu possède des côtés de longueur a et b, leur aire est égale à ab. Comme il existe deux rectangles bleus, on obtient bien la formule annoncée.
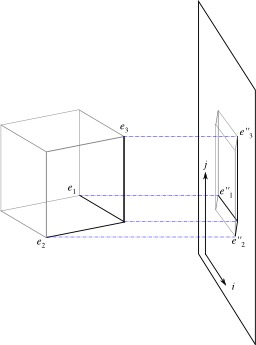
Projection orthogonale
La projection orthogonale est un type de perspective très utilisée en dessin (géométrie descriptive), et en infographie : la génération des figures est simple, par contre, on ne peut pas représenter l'éloignement (la taille des objets ne varie pas avec la distance). De manière plus générale, en algèbre linéaire, une projection orthogonale est un projecteur tel que les deux sous-espaces sont orthogonaux. La projection orthogonale permet de résoudre le problème de la plus courte distance d'un point à une droite, d'un point à un plan, ou plus généralement d'un point à un sous-espace affine d'un espace euclidien d'autre part. On peut alors utiliser ce concept pour résoudre des problèmes de type «moindres carrés». L'idée générale, basée sur le théorème de Pythagore, est que le problème de plus courte distance se ramène à une propriété d'orthogonalité.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
Puissance d'un point
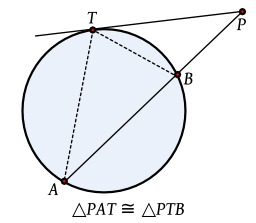
En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
Puissance d'un point
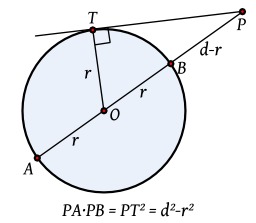
Détermination de la valeur algébrique de la puissance d'un point extérieur à un cercle. En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
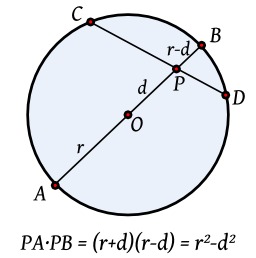
Puissance d'un point intérieur à un cercle
Détermination de la valeur algébrique de la puissance d'un point intérieur à un cercle : PAxPB = (r+d) (r-d).
Série géométrique
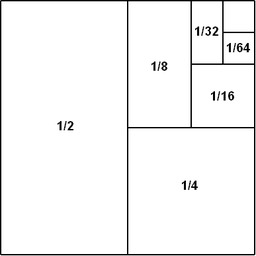
En mathématiques, la série géométrique est l'un des exemples de série numérique les plus simples qu'on puisse donner. C'est la somme des termes d'une suite géométrique. Intuitivement, une série géométrique est une série avec un ratio constant des termes successifs. Par exemple, la série 1/2 + 1/4 + 1/8 + 1/16 + ... est géométrique, parce que chaque terme successif est obtenu en multipliant le terme précédent par 1/2.
Somme des 2 puissance n.
Représentation géométrique d'une somme algébrique : la somme des 2j si j varie de 0 à n.
Dessins et plans, Géométrie, Astronomie, Claude Ptolémée (0100?-0170?), Cercles, Cercles du triangle, Mathématiciens grecs
Théorème de Ptolémée
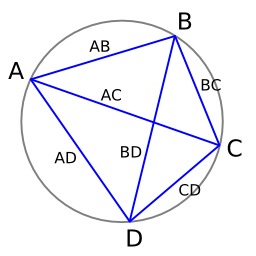
Quadrilatère illustrant le théorème de Ptolémée. Le théorème de Ptolémée est un théorème de géométrie euclidienne. Il décrit une relation algébrique entre les longueurs des côtés et des diagonales d'un quadrilatère, équivalente à l'inscription du quadrilatère dans un cercle. L'implication directe est attribuée à l'astronome et mathématicien grec Ptolémée, dont il se servit pour ses calculs liés à l'astronomie.
Théorème de Ptolémée
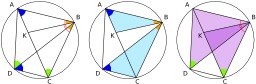
Preuve géométrique du théorème de Ptolémée. Le théorème de Ptolémée est un théorème de géométrie euclidienne. Il décrit une relation algébrique entre les longueurs des côtés et des diagonales d'un quadrilatère, équivalente à l'inscription du quadrilatère dans un cercle.