Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
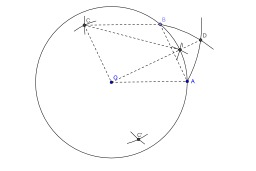
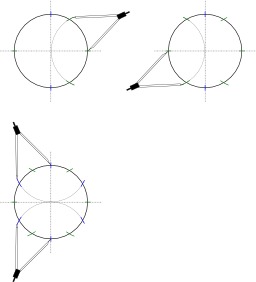
Construction du milieu d'un arc au compas
Construction au compas seul du milieu d'un arc : OABC est un parallélogramme de la forme OA=OB, I est le milieu de l'arc AB de centre O, D est le point de la demi-droite [OI) telle que CA=CD, alors OD=CI. En effet, CD^2=CA^2=2CO^2+OA^2. Ensuite il suffit d'appliquer le théorème de Pythagore dans les deux triangles rectangle COI et COD : CI^2=CO^2+OI^2=CO^2+OA^2, OD^2=CD^2-CO^2=CO^2+OA^2. Or cette figure est réalisable au compas seul et permet donc de placer le point I. Si l'on suppose donnés le point O et l'arc AB, on construit le point C intersection du cercle de centre B et passant par A avec le cercle de centre O et de rayon AB. On construit de même le point C' intersection du cercle de centre A passant par O et du cercle de centre O et de rayon AB. Le point D est à l'intersection des cercles de centre C et C' et passant par A et B. Le point I est à l'intersection des cercles de centre C et C' et de rayon OD.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas
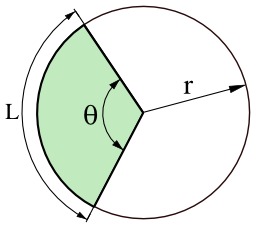
Arc de cercle
Cercle de rayon "r", arc de cercle de longueur "L" soustendu par un angle θ (theta) avec un secteur circulaire de surface "A".
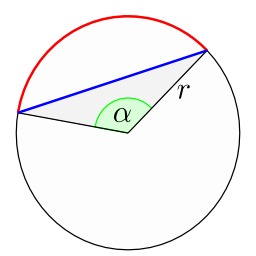
Arc et corde d'un cercle
Un cercle est une courbe plane fermée constituée des points situés à égale distance d'un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Une corde (en bleu) est un segment de droite dont les extrémités se trouvent sur le cercle. Un arc est une portion de cercle délimitée par deux points (en rouge). Un secteur circulaire est une partie du disque comprise entre deux rayons. Un angle au centre (vert) est un angle formé par deux rayons du cercle.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas, Compas,
Couper un cercle en 8
Le tracé d'une bissectrice permet de définir deux arcs égaux, et ici de diviser le cercle en 8 parties égales : placer un point entre chaque point déjà placé : on place la pointe du compas sur un des points et l'on trace un arc de cercle à l'extérieur du cercle de base, et l'on fait de même sur le point voisin ; l'intersection des deux arcs définit un point. Puis, on trace à la règle le diamètre passant par ce point-là ; il coupe l'arc de cercle en deux parts égales (bissectrice de l'angle). Ainsi, si le cercle est déjà coupé en 4 parts, on en obtient 8 ; si le cercle est déjà coupé en 12 parts, on en obtient 24. On peut recouper les arcs en 2 par la même méthode, et multiplier ainsi le nombre d'arcs par 2, pour obtenir encore plus d'arcs.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas
Couper un cercle en douze parties égales
Méthode pour couper un cercle en douze parties égales en trois étapes : Avant de tracer le cercle, on trace les diamètres horizontal et vertical (droites horizontale et verticale passant par le centre) ; ce sont les « traits d'axe du cercle ». Ainsi, lorsque l'on trace le cercle, celui-ci est séparé en 4 quartiers. Pour le séparer en 12 parts égales, on place la pointe du compas sur l'intersection d'un axe et du cercle, tout en gardant un écartement égal au rayon. Puis, on trace les arcs de cercle coupant le cercle. On procède ainsi pour chaque intersection axe-cercle, on obtient au total 12 parts égales.
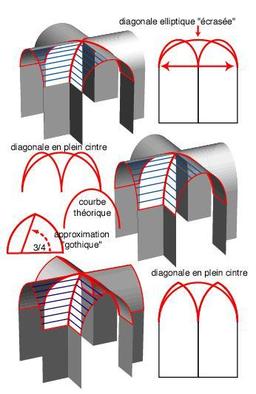
Croisée d'ogives
Genèse de la croisée d'ogives. La projection orthogonale de cette croisée selon l’axe de chacune des nefs donne une demi-ellipse posée dans sa hauteur, très résistante en son sommet. Par chance, il existe une bonne approximation de cet arc pour cette époque où, sur le chantier, à défaut de bons moyens de calcul et de mesures précises il vaut mieux recourir à des tracés simples à exécuter : il s’agit d'un arc brisé composé de deux arcs de cercle centrés respectivement au premier et au troisième quart de la distance à franchir. Cette approximation est souvent observable à une légère déformation de la voûte de la croisée à l'endroit où elle se raccorde aux nefs.
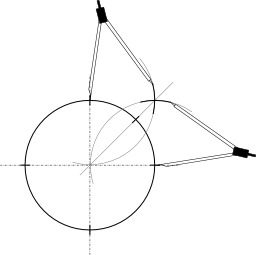
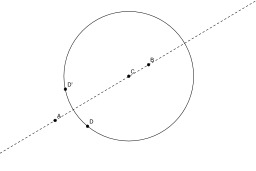
Intersection d'une droite et d'un cercle au compas
Construction au compas seul de l'intersection d'un cercle avec son diamètre : Si la droite (AB) est un diamètre du cercle, et si le point D n'est pas situé sur (AB). On construit de symétrique de D par rapport à (AB). Les deux points à chercher sont les milieux des deux arcs d'extrémités DD'.