Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
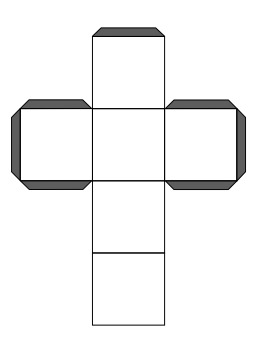
Deux équerres dos à dos
Deux équerres dos à dos, hypothénuse contre hypothénuse, formant un carré.
Carrés géométriques
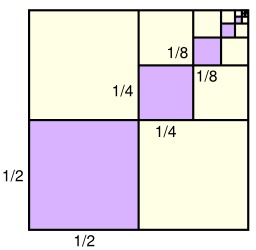
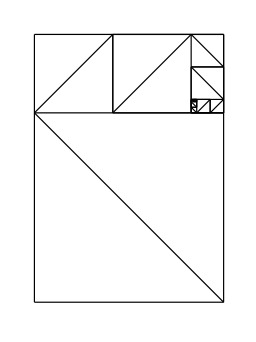
Illustration de l'égalité 1/4 + 1/16 + 1/64 + 1/256 + ⋯ = 1/3 : chacun des carrés violets mesure 1/4 de la surface du grand carré le plus proche (1/2×1/2 = 1/4, 1/4×1/4 = 1/16, etc.). Par ailleurs, la somme des aires des carrés violets est égale à un tiers de la superficie du grand carré.
Connectivité du carré
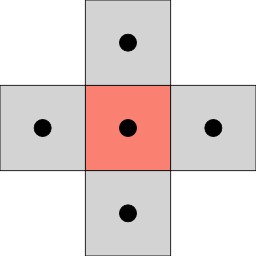
Dans le cadre des pavages, la connectivité géométrique indique la relation entre un élément de pavage (une case ou tuile) et ses voisins. On parlera de 4-connectivité lorsqu'une case (ici un carré) comporte 4 voisins directs.
Connectivité du carré
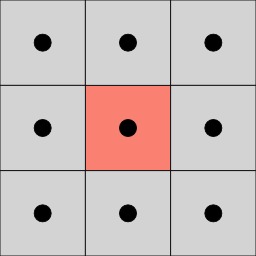
Dans le cadre des pavages, la connectivité géométrique indique la relation entre un élément de pavage (une case ou tuile) et ses voisins. On parlera de 8-connectivité lorsqu'une case (ici un carré) comporte 8 voisins directs.
Dessins et plans, Calcul, Géométrie, Jeux mathématiques, Mathématiciens, Carrés magiques, John Horton Conway (1937-)
Construction d'un carré magique par la méthode du losange - 1
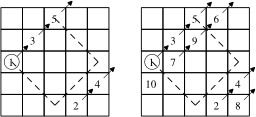
Premières étapes de la construction d'un carré magique 5x5 par la méthode du losange proposée par John Horton Conway : 1) Les nombres impairs 1, 3 et 5 sont inscrits selon une diagonale montante qui va de gauche à droite ; 2) Les nombres pairs 2 et 4 sont ensuite inscrits pour compléter la diagonale brisée ; 3) « Descendre » à la prochaine diagonale ; 4) Recommencer avec les nombres suivants.
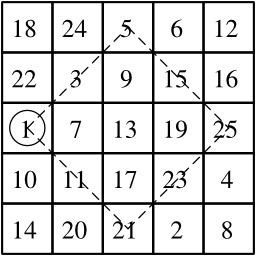
Construction d'un carré magique par la méthode du losange - 2
Un carré magique 5x5 construit selon la méthode du losange proposée par John Horton Conway : Le résultat final est un carré magique dont la constante est 65.
Photographie, Géométrie, Couleurs, Jeux éducatifs, Jeux de dés, Jeux de société, Formes (mathématiques)
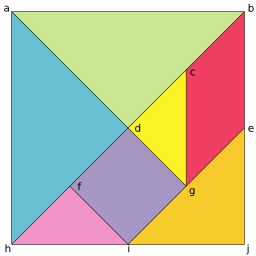
Jeu de formes géométriques
Jeu de plateau "Fits" : association de formes géométriques de couleur. Jeu créé par Charles B. Phillips et Ronald Wiecek en 1999 et édité par Ravensburger. Pour 2 à 4 joueurs, à partir de 8 ans, pour environ 5 à 15 minutes. Les joueurs cherchent à compléter une planche carrée à l'aide d'éléments géométriques de couleurs différentes le plus vite possible, tout en respectant des règles de placement relatives aux lignes de la planche et aux couleurs. Matériel : 4 planches de jeu, un support de pièces proposant 5 piles de pièces (2 pour chaque taille de triangle et 1 pour les carrés), 80 pièces de 4 couleurs différentes (rouge, jaune, vert et bleu) réparties de la manière suivante : 32 grands triangles, 32 petits triangles, 16 carrés ; et un dé spécial (2 faces "petit triangle", 2 faces "grand triangle", 1 face "carré" et 1 face "main").
Dessins et plans, Géométrie, Couleurs, Tapis, Carré, Mathématiciens, Savants polonais, Wacław Sierpinski (1882-1969), Fractales
Le carré de Sierpinski
Le tapis de Sierpiński (1916), du nom de Wacław Sierpiński (1882-1969), est une fractale obtenue à partir d'un carré. Le tapis se fabrique en découpant le carré en neuf carrés égaux avec une grille de trois par trois, et en supprimant la pièce centrale, et en appliquant cette procédure indéfiniment aux huit carrés restants.
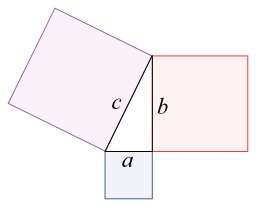
Le théorème de Pythagore
Version géométrique du théorème de Pythagore, le théorème fondamental des espaces euclidiens : la somme des surfaces des deux carrés rose et bleu est égale à la surface du carré violet dont le côté est l'hypothénuse.
Gravure, Géométrie, Albrecht Dürer (1471-1528), Symbolisme dans l'art, Carrés magiques, Attributs (symbolisme), Mélancolie
Mélancolie
Melencolia ou La Melencolia est le nom donné à une gravure sur cuivre d'Albrecht Dürer datée de 1514. Le titre est pris de l'œuvre où il apparaît comme un élément de la composition. Melencolia I est souvent considéré comme faisant partie d'une série, Meisterstiche, comprenant également Le chevalier, la mort et le diable (1513) et Saint Jérôme dans sa cellule (1514). Cette œuvre d'une richesse symbolique exceptionnelle a été l'objet d'un nombre considérable d'études. Source : http://fr.wikipedia.org/wiki/Melencolia_I.
Photographie, Géométrie, Antiquités gallo-romaines, Octogones, Formes (mathématiques), Mosaïques, Bordeaux (Gironde) -- Musée d'Aquitaine, sylvanus-aquitaine
Mosaïque géométrique de Burdigala
Mosaïque géométrique de Burdigala : motif d'octogone et de huit carrés adjacents.
Pavage jaune, bleu et vert
Pavage régulier obtenu avec deux formes géométriques, un carré (jaune) et un triangle (bleu, vert).
Pliage fractal 02 en Origami
Pliage fractal 02 en origami : dans le rectangle restant, aux mêmes proportions que le premier, il est encore possible de retirer deux carrés, puis de recommencer, théoriquement jusqu'à l'infini.
Projection orthogonale
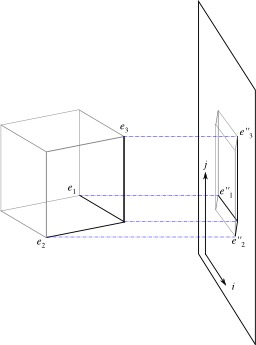
La projection orthogonale est un type de perspective très utilisée en dessin (géométrie descriptive), et en infographie : la génération des figures est simple, par contre, on ne peut pas représenter l'éloignement (la taille des objets ne varie pas avec la distance). De manière plus générale, en algèbre linéaire, une projection orthogonale est un projecteur tel que les deux sous-espaces sont orthogonaux. La projection orthogonale permet de résoudre le problème de la plus courte distance d'un point à une droite, d'un point à un plan, ou plus généralement d'un point à un sous-espace affine d'un espace euclidien d'autre part. On peut alors utiliser ce concept pour résoudre des problèmes de type «moindres carrés». L'idée générale, basée sur le théorème de Pythagore, est que le problème de plus courte distance se ramène à une propriété d'orthogonalité.
Dessins et plans, Carré, Surfaces (mathématiques) -- Volumes, Géométrie des nombres, Johann Faulhaber (1580-1635), Pyramides (géométrie)
Somme des carrés
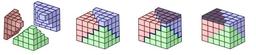
Un exemple de preuve sans mots à propos de la somme des premiers carrés : chacune des trois pyramides a pour volume la somme des carrés de 1 à n (n=4 dans cette illustration) ; le parallélépipède final est de côtés n, n+1 et n+1/2. Ce résultat se généralise pour la somme des n premières puissances strictement positives. Cette somme porte le nom de formule de Faulhaber. Johann Faulhaber (1580-1635) est un mathématicien allemand qui collabora avec Kepler.
Photographie, Abeilles mellifères, Géométrie, Miel, Hexagones, Polygones, Agriculture, Produits du rucher, Structures en nids d'abeilles
Structure hexagonale des rayons de miel
Les hexagones réguliers peuvent se juxtaposer les uns les autres sans laisser aucune lacune, comme les carrés et les triangles équilatéraux, et sont ainsi utiles pour construire des pavages. Les cellules des rayons dans une ruche d'abeilles à miel sont hexagonales pour cette raison et parce que cette forme permet une utilisation efficace de l'espace et des matériaux de construction.