Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Équations, Identités remarquables, Équations -- Solutions numériques, Équations algébriques, Équations du second degré
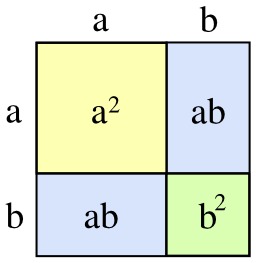
Identité remarquable du second degré
Identité remarquable du second degré : équation (a+b)^2=a^2 + 2ab + b^2. Pour se convaincre de la véracité de la formule, on considère cette figure qui représente un carré. On suppose que la longueur côté du carré jaune est égale à a et celle du carré vert à b. L'aire du grand carré est égale à (a + b)^2. Il existe une autre manière d'exprimer cette aire, elle est la somme des aires jaune, verte et des deux zones bleues. L'aire jaune est égale à a^2 car c'est un carré de côté a, l'aire verte est égale à b^2 et chaque rectangle bleu possède des côtés de longueur a et b, leur aire est égale à ab. Comme il existe deux rectangles bleus, on obtient bien la formule annoncée.